Users Guide
The Structure of PGAPack
This chapter provides a general overview of the structure of PGAPack.
Native Data Types
PGAPack is a data-structure-neutral library. By this we mean that a data-hiding capability provides the full functionality of the library to the user, in a transparent manner, irrespective of the data type used. PGAPack supports four native data types: binary-valued, integer-valued, real-valued, and character-valued strings. In addition, PGAPack is designed to be easily extended to support other data types (see Chapter Custom Usage: Native Data Types).
The binary (or bit) data type (i.e., |1|0|1|1|) is the traditional
GA coding. The bits may either be interpreted literally or decoded into
integer or real values by using either binary coded decimal or
binary-reflected Gray codes. In PGAPack the binary data type is
implemented by using each distinct bit in a computer word as a gene,
making the software very memory-efficient. The integer-valued data type
(i.e., |3|9|2|4|) is often used in routing and scheduling problems.
The real-valued data type (i.e., |4.2|7.1|-6.3|0.8|) is useful in
numerical optimization applications. The character-valued data type
(i.e., |h|e|l|l|o|w|o|r|l|d|is useful for symbolic applications.
Context Variable
In PGAPack the context variable is the data structure that provides the data hiding capability. The context variable is a pointer to a C language structure, which is itself a collection of other structures. These (sub)structures contain all the information necessary to run the genetic algorithm, including data type specified, parameter values, which functions to call, operating system parameters, debugging flags, initialization choices, and internal scratch arrays. By hiding the actual data type selected and specific functions that operate on that data type in the context variable, user-level functions in PGAPack can be called independent of the data type.
Almost all fields in the context variable have default values. However, the user can set values in the context variable by using the PGASet family of function calls. The values of fields in the context variable may be read with the PGAGet family of function calls.
Levels of Usage Available
PGAPack provides multiple levels of control to support the requirements
of different users. At the simplest level, the genetic algorithm
“machinery” is encapsulated within the PGARun() function, and the user
need specify only three parameters: the data type, the string length,
and the direction of optimization. All other parameters have default
values. At the next level, the user calls the data-structure-neutral
functions explicitly (e.g., PGASelect(), PGACrossover(),
PGAMutate()).
This mode is useful when the user wishes more explicit control over the
steps of the genetic algorithm or wishes to hybridize the genetic
algorithm with a hill-climbing heuristic. At the third level, the user
can customize the genetic algorithm by supplying his or her own
function(s) to provide a particular operator(s) while still using one of
the native data types. Finally, the user can define his or her own
datatype, write the data-structure-specific low-level GA functions for
the datatype (i.e., crossover, mutation, etc.), and have the
data-structure-specific functions executed by the high-level
data-structure-neutral PGAPack functions.
Function Call-Based Library
All the access to, and functionality of, the PGAPack library is provided through function calls.
The PGASet family of functions sets parameter values, allele values, and specifies which GA operators to use. For example,
PGASetPopSize (ctx, 500)sets the GA population size to 500.The PGAGet family of functions returns the values of fields in the context variable and allele values in the string. For example,
bit = PGAGetBinaryAllele (ctx, p, pop, i)returns the value of theith bit in stringpin populationpopintobit.The simplest level of usage is provided by the
PGARun()function. This function will run the genetic algorithm by using any nondefault values specified by the user and default values for everything else.The next level of usage is provided by the data-structure-neutral functions, which the user can call to have more control over the specific steps of the genetic algorithm. Some of these functions are
PGASelect(),PGACrossover(),PGAMutate(),PGAEvaluate(), andPGAFitness().The data-structure-specific functions deal directly with native data types. In general, the user never calls these functions directly.
System calls in PGAPack provide miscellaneous functionality, including debugging, random number generation, output control, and error reporting.
Header File and Symbolic Constants
The PGAPack header file contains symbolic constants and type definitions
for all functions and should be included in any file (or function or
subroutine in Fortran) that calls a PGAPack function. For example,
PGA_CROSSOVER_UNIFORM is a symbolic constant that is used as an
argument to the function PGASetCrossoverType() to specify uniform
crossover. In C the header file is pgapack.h. In Fortran it is
pgapackf.h
Evaluation Function
PGAPack requires that the user supply a function that returns an evaluation of a string that it will map to a fitness value. This function is called whenever a string evaluation is required. The calling sequence and return value of the function must follow the format discussed in Section String Evaluation and Fitness.
Parallelism
PGAPack can be run on both sequential computers (uniprocessors) and parallel computers (multiprocessors, multicomputers, and workstation networks). The parallel programming model used is message passing, in particular the single program, single data (SPMD) model. PGAPack supports sequential and parallel implementations of the global population model (see Chapter Parallel Aspects).
Implementation
PGAPack is written in ANSI C. A set of interface functions allows most user-level PGAPack functions to be called from Fortran. All message-passing calls follow the Message Passing Interface (MPI) standard [MPI94], [GLS94], [MPI21]. Nonoperative versions of the basic MPI functions used in the examples are supplied if the user does not provide an MPI implementation for their machine. These routines simply return and provide no parallel functionality. Their purpose is to allow the PGAPack library to be built in the absence of an MPI implementation.
Most low-level internal functions in PGAPack are data-structure specific and use addresses and/or offsets of the population data structures. The user-level routines, however, provide the abstractions of data-structure neutrality and an integer indexing scheme for access to population data structures.
Basic Usage
As the examples in Chapter Examples show, a PGAPack program can be written with just four function calls and a string evaluation function. This basic usage is discussed further in Section Required Functions. Sections Stopping Criteria to Utility Functions explain options available in PGAPack. Section Command-Line Arguments discusses PGAPack command line arguments.
Required Functions
Any file (or function or subroutine in C and Fortran) that uses a
PGAPack function must include the PGAPack header file. In C this file is
pgapack.h. In Fortran this file is pgapackf.h. The first
PGAPack call made is always to PGACreate(). In C this call looks
like
PGAContext *ctx;
ctx = PGACreate (&argc, argv, datatype, len, maxormin);
PGACreate() allocates space for the context variable, ctx
(Section Context Variable), and returns its address. argc and
argv are the standard list of arguments to a C program. datatype
must be one of the constants defined in group Constants for Datatypes
to specify strings
consisting of binary-valued, integer-valued, real-valued,
character-valued or user-defined strings, respectively.
The parameter len is the length of the
string (i.e., the number of genes), maxormin must be one in group
Constants for Optimization Direction to indicate whether the user’s
problem is maximization or minimization, respectively.
In Fortran the call to PGACreate() is
integer ctx
ctx = PGACreate (datatype, len, maxormin)
where datatype, len, and maxormin are the same as for C
programs. After the PGACreate() call, the user may optionally set
nondefault values. These are then followed by a call to PGASetUp() to
initialize to default values all options, parameters, and operators not
explicitly specified by the user. For example,
ctx = PGACreate (&argc, argv, datatype, len, maxormin);
PGASetPopSize (ctx, 500);
PGASetFitnessType (ctx, PGA_FITNESS_RANKING);
PGASetCrossoverType (ctx, PGA_CROSSOVER_UNIFORM);
PGASetUniformCrossoverProb (ctx, 0.6);
PGASetUp (ctx);
will change the default values for the population size, the mapping of
the user’s evaluation to a fitness value, and the crossover type. All
PGASet calls should be made after PGACreate()
has been called,
but before PGASetUp() has been called; all such calls are
optional. Note also that all PGAPack functions other than
PGACreate() take the context variable as their first argument.
The PGARun() function executes the genetic algorithm. Its second
argument is the name of a user-supplied evaluation function that returns
a double (double precision in Fortran) value that is the user’s
evaluation of an individual string. In C the prototype for this function
looks like
double evaluate (PGAContext *ctx, int p, int pop, double *aux);
and in Fortran
double precision function evaluate (ctx, p, pop, aux)
integer ctx, p, pop
double precision aux(*)
The user must write the evaluation function, and it must have the
calling sequence shown above and discussed further in
Section String Evaluation and Fitness, except that depending on the
architecture and the calling convention of the compiler, the aux
argument can be left out. After PGARun() terminates,
PGADestroy() is called to release all memory allocated by
PGAPack. 1
Except for writing an evaluation function (Section String Evaluation and Fitness) the information contained in rest of this chapter is optional—defaults will be set for all other GA parameters. We do note, however, that the defaults used are the result of informal testing and results reported in the GA literature. They are by no means optimal, and additional experimentation with other values may well yield better performance on any given problem.
Population Replacement
PGAPack supports several different population replacement schemes. Among them the two most common replacement schemes in the literature. The first, the generational replacement genetic algorithm (GRGA), replaces the entire population each generation and is the traditional genetic algorithm [Hol92]. The second, the steady-state genetic algorithm (SSGA), typically replaces only a few strings each generation and is a more recent development [Sys89], [Whi89], [WK88]. A third scheme, originally called restricted tournament selection by Harik [Har94], [Har95] and later adopted under the name of restricted tournament replacement by Pelikan [Pel05] replaces offspring candidates into the original population by selecting a number of members from the original population and selecting the member most similar to the candidate. The similarity metric is implemented by a genetic distance function see section Basics. The candidate is then compared to the most similar member and only if the new solution candidate is better than the member it replaces it. This approach is repeated for each new solution. A fourth approach used by evolutionary algorithm variants that mutate an individual into an offspring that replaces its parent only when it is better is also supported. This variant is used by the popular Differential Evolution [SP95], [SP97], [PSL05] algorithm. We call this replacement variant pairwise best in the following. Individuals with the same index in the old and the new population are compared and the one with the better fitness is used.
Two algorithms are typically used for multi-objective optimization. The
first one is the elitist Nondominated Sorting Genetic Algorithm
(Version 2), NSGA-II [DPAM02] and is called NSGA-II
replacement. It can be used for single-objective optimization, too, both
with and without constraints. If constraints are present, by default the
constraint violations are summed. An alternative is to use nondominated
sorting for constraints, too. This can be switched on by setting
PGASetSumConstraintsFlag() to PGA_FALSE.
The second is the Nondominated Sorting Genetic Algorithm for many-objective optimization, NSGA-III [DJ14], [JD14]. NSGA-II and NSGA-III are the only possible population replacement algorithms when using multi-objective optimization.
With NSGA-III you need to define a regular set of points or a set of directions where you want solutions to the multi-objective problem to be found, both can be combined, you can specify both, a number of reference directions and reference points. The reference points are in a hyperplane defined by the M positive axes of the objective space, the hyperplane goes through the axes intercepts at coordinate 1 for each of the axes. An example for three objectives with a partition size of 12 is shown in figure Reference points in 3 dimensions, partition-size 12.
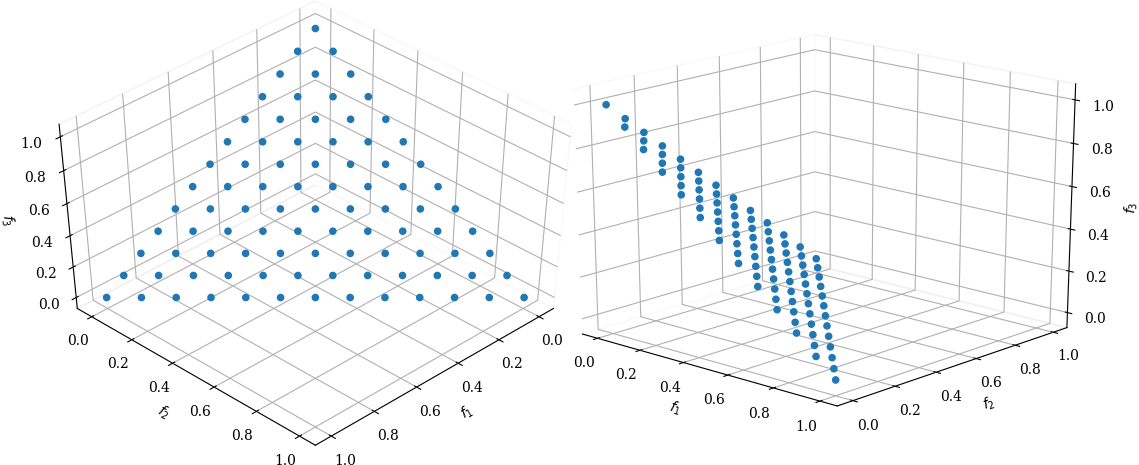
Reference points in 3 dimensions, partition-size 12
The discovered pareto-front is projected onto this hyperplane [BDR19]. When specifying reference directions, these are directly defined in the objective space (without any projection).
To compute a set of points we use an algorithm originally defined in a
paper by I. Das and J. E. Dennis [DD98] with the
function LIN_dasdennis(). This function gets the dimension (the number
of objectives to optimize which is the number of auxiliary evaluations
+1 minus the number of constraints) and the number of partitions. It
returns the points in result and optionally takes a scale factor in
the range 0..1 and a direction to shift this scaled set of points. The
direction is only needed if the scale factor is less than one. The first
time the function is called, the result must point at a NULL pointer.
The function automatically allocates the necessary memory. It can be
called multiple times to extend the points already allocated. The
resulting points are then passed into the function
PGASetReferencePoints():
int npoints = 0;
void *result = NULL;
double point [3] = {1, 1, 1};
PGASetNumAuxEval (ctx, 2);
PGASetNumConstraint (ctx, 0);
npoints = LIN_dasdennis (3, 2, &result, 0, 1, NULL);
npoints = LIN_dasdennis (3, 1, &result, npoints, 0.5, point);
PGASetReferencePoints (ctx, npoints, result);
For defining reference directions, the function
PGASetReferenceDirections() is used. It gets the number of directions
and the vector of directions (each direction is a vector of the
dimensionality of the number of objectives) and the number of partitions
(for Das/Dennis points) and the scale factor of the generated points:
double directions [][3] = {{1, 1, 1}, {1, 2, 3}};
PGASetReferenceDirections (ctx, 2, directions, 12, 0.05);
The difference to the reference points above is that the reference directions are in the objective space and the Das/Dennis points are generated dynamically in each generation.
Note that by default when no population size if specified, NSGA-III uses the number of points defined by the reference points and reference directions for the population size.
The NSGA-III replacement optimizes the solutions to be near the reference points and/or reference directions. With a high number of objective functions, the N-dimensional space forming the solution space increases exponentially with the number of objective functions. This is known as the “curse of dimensionality”. With NSGA-II it is increasingly hard to find a well distributed set of solutions with more than two or three objectives. With the NSGA-III replacement it is possible to concentrate the search to a predefined number of reference points or reference directions.
PGAPack supports both GRGA and SSGA and variants in between via parameterized population replacement. For example, the PGASet calls
PGASetPopSize (ctx, 200);
PGASetNumReplaceValue (ctx, 10);
PGASetPopReplaceType (ctx, PGA_POPREPL_BEST);
specify that each generation a new population is created consisting of
ten strings created via recombination, and the 190 most fit strings from
the old population. The 190 strings can also be selected randomly, with
or without replacement, by setting the second argument of
PGASetPopReplaceType() to PGA_POPREPL_RANDOM_REP or
PGA_POPREPL_RANDOM_NOREP, respectively.
For selecting restricted tournament replacement PGA_POPREPL_RTR is
used. The default for the window size (number of members of the old
population that are chosen for comparison with a new candidate) is
min \((n, N/20)\) where \(n\) is the string length and \(N\)
is the population size [Pel05]. The window size can be
set or queried with PGASetRTRWindowSize() and
PGAGetRTRWindowSize(),
respectively. Note that when restricted tournament replacement is in
use, the maximum number of new candidates is limited with the number set
with PGASetNumReplaceValue() but fewer—depending on fitness–may be
replaced into the new population. Note that it depends on the selection
which individuals in the old population are replaced. Since restricted
tournament replacement is an elitist strategy the overall fitness never
dimishes with this replacement strategy.
For pairwise best replacement PGA_POPREPL_PAIRWISE_BEST is used as
the replacement type. Like restricted tournament replacement it is an
elitist strategy.
For NSGA-II replacement PGA_POPREPL_NSGA_II is used. For NSGA-III
replacement PGA_POPREPL_NSGA_III is used. The number of auxiliary
evaluation function can be set with PGASetNumAuxEval() and the number
of constraints can be set with PGASetNumConstraint(). If the
difference between the two is \(>0\) (i.e. the number of objectives
is \(>1\)), these auxiliary evaluations are used for multi-objective
optimization. Only the NSGA-II and NSGA-III replacement are possible
with these settings (i.e. when the number of objectives is \(>1\)).
The replacement types pairwise best, restricted tournament replacement, NSGA-II, and NSGA-III replacement have selection pressure in addition to providing a population replacement strategy. So these can be used if a selection scheme without selection pressure (a tournament strategy with only one participant in the tournament or linear selection) is used.
By default, the number of new strings created each generation is 10
percent of the population size (an SSGA population replacement
strategy). A GRGA can be implemented by setting
PGASetNumReplaceValue() to the population size (the default population
size is 100). Setting PGASetNumReplaceValue() to one less than the
population size will result in an elitist GRGA, where the most fit
string is always copied to the new population (since
PGA_POPREPL_BEST is the default population replacement strategy).
Traditionally, strings created through recombination first undergo crossover and then mutation. Some practitioners [Dav91] have argued that these two operators should be separate. By default, PGAPack applies mutation only to strings that did not undergo crossover.
This is equivalent to setting PGASetMixingType() to
PGA_MIX_MUTATE_OR_CROSS which is also the default. To have strings
undergo both crossover and mutation, one should set
PGASetMixingType() to PGA_MIX_TRADITIONAL. Note that
there is also a mode that will not mutate strings that are not also
crossed over. This can be enabled by setting PGASetMixingType()
to PGA_MIX_MUTATE_AND_CROSS.
If an evolutionary algorithm variant without crossover is used or if
special crossover techniques with more that two parents should be
applied, all the logic can be implemented in a custom crossover operator
and the PGASetMixingType() can be set to
PGA_MIX_MUTATE_ONLY. In this mode no crossover is performed
at all.
There is also a legacy interface which should not be used for new
code. Functions used in that interface are:
PGASetMutationOrCrossoverFlag(),
PGASetMutationAndCrossoverFlag(),
and PGASetMutationOnlyFlag().
By default, PGAPack allows duplicate strings in the population. Some
practitioners advocate not allowing duplicate strings in the population
in order to maintain diversity. The function call
PGASetNoDuplicatesFlag() with the parameters (ctx, PGA_TRUE)
will not allow duplicate
strings in the population: It repeatedly applies the mutation operator
(with an increasing mutation rate) to a duplicate string until it no
longer matches any string in the new population. If the mutation rate
exceeds 1.0, however, the duplicate string will be allowed in the
population, and a warning message will be issued.
Figure Population Replacement shows the generic population
replacement scheme in PGAPack. Both populations \(k\) and
\(k+1\) are of fixed size (the value returned by PGAGetPopSize()).
First, PGAGetPopSize() - PGAGetNumReplaceValue()
strings are copied
over directly from generation \(k\). The way the strings are chosen,
the most fit, or randomly with or without replacement, depends on the
value set by PGASetPopReplaceType(). The remaining
PGAGetNumReplaceValue() strings are created by crossover and mutation.
Population Replacement
Stopping Criteria
PGAPack terminates when at least one of the stopping rule(s) specified has been met. The three stopping rules are (1) iteration limit exceeded, (2) population too similar, and (3) no change in the best solution found in a given number of iterations. The default is to stop when the iteration limit (by default, 1000 iterations) is reached. Note that when \(\epsilon\)-constraint optimization is in use, stopping is not triggered as long as \(\epsilon>0\), see section String Evaluation and Fitness.
The choice of stopping rule is set by PGASetStoppingRuleType(). For
example, PGASetStoppingRuleType() with parameters
(ctx, PGA_STOP_MAXITER) is the
default. Other choices are PGA_STOP_TOOSIMILAR and
PGA_STOP_NOCHANGE for population too similar and no change in the
best solution found, respectively. PGASetStoppingRuleType() may be
called more than once. The different stopping rules specified are
ored together.
If PGA_STOP_MAXITER is one of the stopping rules,
PGASetMaxGAIterValue() with parameters (ctx, 500)
will change the maximum iteration limit to 500. If
PGA_STOP_NOCHANGE is one of the stopping rules,
PGASetMaxNoChangeValue() with parameters (ctx, 50) will
change from 100 (the default) to 50 the maximum number of iterations in
which no change in the best evaluation is allowed before the GA stops.
If PGA_STOP_TOOSIMILAR is one of the stopping rules,
PGASetMaxSimilarityValue() with parameters (ctx, 99) will
change from 95 to 99 the percentage of the population allowed to have
the same evaluation function value before the GA stops.
Initialization
Strings are either initialized randomly (the default), or set to zero.
The choice is specified by setting the second argument of
PGASetRandomInitFlag() to either PGA_TRUE or
PGA_FALSE, respectively. Random initialization depends on the
datatype.
If binary-valued strings are used, each gene is set to 1 or 0
with an equal probability. To set the probability of randomly setting a
bit to 1 to 0.3, use PGASetBinaryInitProb() with parameters
(ctx, 0.3).
For integer-valued strings, the default is to set the strings to a
permutation on a range of integers. The default range is
\([0,L-1]\), where \(L\) is the string length.
PGASetIntegerInitPermute() with parameters (ctx, 500, 599)
will set the permutation
range to \([500,599]\). The length of the range must be the same
as the string length.
Alternatively, PGASetIntegerInitRange() will set each gene to a random
value selected uniformly from a specified range. For example, the code
stringlen = PGAGetStringLength (ctx);
for (i=0;i<stringlen;i++) {
low[i] = 0;
high[i] = i;
}
PGASetIntegerInitRange (ctx, low, high);
will select a value for gene i uniformly randomly from the interval
\([0,i]\).
If real-valued strings are used, the alleles are set to a value selected
uniformly randomly from a specified interval. The interval may be
specified with either the PGASetRealInitRange() or
PGASetRealInitFraction() functions. For example, the code
stringlen = PGAGetStringLength (ctx);
for (i=0; i<stringlen; i++) {
low[i] = -10.0;
high[i] = (double) i;
}
PGASetRealInitRange (ctx, low, high);
will select a value for allele i uniformly randomly from the
interval \([-10.0,{\tt i}]\). This is the default strategy for
initializing real-valued strings. The default interval is
\([0,1.0]\).
PGASetRealInitFraction() specifies the interval with a median
value and fraction of the median as offset. For example,
stringlen = PGAGetStringLength (ctx);
for (i=1; i<=stringlen; i++) {
median [i-1] = (double) i;
percent [i-1] = .5;
}
PGASetRealInitFraction (ctx, median, percent);
will select a value for allele i uniformly randomly from the
increasing intervals \([\frac{1}{2}i,\frac{3}{2}i]\). Note that if
the median value is zero for some \(i\), then an interval of
\([0,0]\) will be defined.
If character-valued strings are used,
PGASetCharacterInitType() with parameters (ctx, PGA_CINIT_UPPER)
will set the allele
values to uppercase alphabetic characters chosen uniformly randomly.
Other options are PGA_CINIT_LOWER for lower case letters only (the
default) and PGA_CINIT_MIXED for mixed case letters, respectively.
Selection
The selection phase allocates reproductive trials to strings on the basis of their fitness. PGAPack supports five selection schemes: proportional selection, stochastic universal selection, truncation selection, tournament selection (default is binary tournament selection), and probabilistic binary tournament selection. A sixth scheme which is called linear selection that is not a selection scheme in the genetic sense (it has no selection pressure) is used for evolutionary algorithms that rely on modification of individuals that later replace their parent if the offspring has higher fitness, so the selection pressure is applied in the replacement strategy. The linear scheme is guaranteed to return individuals in population order.
The choice may be specified by setting the second argument of
PGASetSelectType() to one of the constants in group
Constants for Selection Types. The default is tournament selection. For
tournament selection, the size of the tournament (number of
participants) can be set e.g., with PGASetTournamentSize() with
parameters (ctx, 3).
The default is binary tournament (size = 2). To allow a more
fine-grained selection pressure, the tournament size is a floating-point
value. The integer part of that value specifies the minimum tournament
size. For each tournament for the fractional part, a biased coin is
flipped (using PGARandomFlip()) and the tournament size is increased
by one if the outcome is positive. This mechanism for fine-grained
tournaments was first proposed by Harik and Goldberg
[HG96] and later rediscovered by Filipović et. al. [FKTL00].
Note that with a tournament size of 1 (or with the linear selection scheme) there is no selection pressure. Having no selection pressure in this step can be compensated by using a replacement scheme with selection pressure, i.e., one of restricted tournament replacement or pairwise best replacement, see section Population Replacement for details on population replacement. If no selection pressure is used in the selection scheme and in the population replacement strategy, the genetic search degenerates to a random walk.
In addition, for tournament selection it can be specified if the
selection is with or without replacement using the function
PGASetTournamentWithReplacement() with a parameter of
PGA_FALSE or PGA_TRUE. Sampling without
replacement guarantees that for \(n\) tournaments, each individual
participates in the same number of tournaments (as long as \(n\)
multiplied by the tournament size is a multiple of the population size)
[GKD89]. This was later re-invented by Sokolov and Whitley under the
name Unbiased Tournament Selection [SW05].
The default sampling is with replacement as if
PGASetTournamentWithReplacement() had been called with the parameter
PGA_TRUE. The probabilistic tournament selection is always binary
(two participants in the tournament), the default probability that the
string that wins the tournament is selected is 0.6. It may be set to
0.8, for example, with PGASetPTournamentProb() with parameters
(ctx, 0.8). The
tournament for probabilistic tournament selection is always with
replacement. The truncation selection by default selects half of the
population. This proportion of selected individuals can be set with
PGASetTruncationProportion() for which the default value is 0.5.
When using multi-objective optimization with, e.g., the NSGA-II [DPAM02] population replacement (see section Population Replacement), it is possible to either use a selection scheme with or without selection pressure. However, selection schemes that rely on direct comparison of individuals (e.g. tournament selection) will sort by the domination rank of the individuals established by the NSGA-II algorithm. This is because for multi-objective optimization there is no full order established by multiple objectives as would be the case for single-objective optimization. This may result in less selection pressure because multiple individuals will typically have the same rank. This lower selection pressure is compensated by the selection pressure introduced by the NSGA-II (or -III) population replacement algorithm.
Most selection schemes (except stochastic universal selection) already
return a randomized sequence. In previous implementations all
sequences got an additional randomization step. By default this is no
longer the case (exect for PGA_SELECT_SUS). You can enable the
previous behavior by setting it to PGA_TRUE with
PGASetRandomizeSelect(). Note that even with this flag set, the
sequence returned by the linear selection scheme is never randomized.
This has adverse effects on crossover with linear selection: With this
scheme the same two adjacent population members are always crossed over
which makes crossover almost ineffective. Linear selection is typically
only useful when using special mutation operators most often with
PGASetMixingType() set to PGA_MIX_MUTATE_ONLY. If you
need a randomized sequence without selection pressure, use tournament
selection without replacement with a tournament size of one.
Crossover
The crossover operator takes bits from each parent string and combines
them to create child strings. The type of crossover may be specified by
setting PGASetCrossoverType() to one of the constants in group
Crossover Constants. The possible crossover types are
one-point, two-point, uniform, or simulated
binary (SBX) crossover, respectively. For integer alleles there is also
Edge Recombination crossover
[WSS91]. If the integer gene is initialized to be a
permutation, this variant preserves this property. In addition some
edges can be defined to be fixed (unmutable). This is done with the
PGAIntegerSetFixedEdges(). An example is given in
examples/sequence.
The default is two-point crossover. By default the crossover rate is
0.85. It may be set to 0.6 by PGASetCrossoverProb() with
parameters (ctx, 0.6), for example. Simulated binary crossover is
available only for integer and real genes.
Uniform crossover and simulated binary crossover are parameterized by
\(p_u\), the probability of swapping two parent bit values
[SD91] in the case of uniform crossover and for
mutating an allele for SBX. By default, \(p_u = 0.5\). The function
call PGASetUniformCrossoverProb() with parameters (ctx, 0.7)
will set \(p_u = 0.7\).
SBX uses a polynomial distribution with a parameter \(\eta_c\) that
defines how far the child may deviate from each parent. For high values
of this parameter, children stay nearer to the parents
[DA95]. Recommended values of this parameter are
typically in the range 2–5, the default is 2 and a different value can
be set with PGASetCrossoverSBXEta().
When crossing strings with SBX, typically for each allele a new random
number is computed for the polynomial distribution. With
PGASetCrossoverSBXOncePerString() you can define that a random number
is only drawn once for each individual to be crossed over. This ensures
that the child is on the line in N-dimensional space between the two
parents if all alleles are crossed over. This may be beneficial when
handling optimization problems that are not decomposable [Sal96]
similar to the crossover rate in differential evolution [PSL05].
Crossover types that may yield child individuals outside the range of
the parents (currently only SBX) may want to call
PGASetCrossoverBoundedFlag() or
PGASetCrossoverBounceBackFlag() with
the context variable and PGA_TRUE to select an algorithm that keeps
the child alleles within the bounds of the initialization ranges of the
gene for each allele. These parameters work analogous to
PGASetMutationBoundedFlag() and PGASetMutationBounceBackFlag()
for mutation. For the bounce-back implementation the parent nearer to
the initialisation boundary is used for each check.
Negative Assortative Mating
When selecting parents for crossover, the default is to use the two
parents chosed by the selection scheme in use, see section
selection. It was observed early [ES91] that genetic diversity
can be maintained (avoiding premature convergence) by enforcing a lower
bound on the genetic distance of parents. Later Fernandes and Rosa
researched several variants of mating restrictions [FR01]. The negative
assortative mating (NAM) selects the first parent as usual but draws a
set of candidate second parents of which the one with the largest
genetic distance to the first parent is selected. The window size for
this set can be set with PGASetNAMWindowSize(), a minimum of two
and a maximum of the population size minus two should be selected to
turn this feature on. The default is to use the standard selection
(window size 1). Originally Fernandes and Rosa used the hamming distance
for computing the genetic distance, but they also investigated an
application specific metric [FTMR01]. PGAPack uses the genetic
distance, see Basics which by default uses the hamming
distance for binary genes and the manhattan distance for integer and
real genes.
The negative assortative mating is for selection what the restricted tournament replacement scheme is for replacement: The latter selects the genetically closest individual for replacement which also results in preserving genetic diversity.
Mutation
The mutation rate is the probability that a gene will undergo
mutation. The mutation rate is independent of the datatype used. The
default mutation rate is the reciprocal of the string length. The
function call PGASetMutationProb() with parameters (ctx, .001)
will set the mutation rate to .001.
The type of mutation depends on the data type. For binary-valued strings, mutation is a bit complement operation. For character-valued strings, mutation replaces one alphabetic character with another chosen uniformly randomly. The alphabetic characters will be lower, upper, or mixed case depending on how the strings were initialized.
For integer-valued strings, if the strings were initialized to a permutation and gene \(i\) is to be mutated, the default mutation operator swaps gene \(i\) with a randomly selected gene. If the strings were initialized to a random value from a specified range and gene \(i\) is to be mutated, by default gene \(i\) will be replaced by a value selected uniformly random from the initialization range.
The mutation operator for integer-valued strings may be changed
irrespective of how the strings were initialized. If
PGASetMutationType() is set to PGA_MUTATION_RANGE,
gene \(i\) will be replaced with a value selected uniformly randomly
from the initialization range. If the strings were initialized to a
permutation, the minimum and maximum values of the permutation define
the range. If PGASetMutationType() is set to
PGA_MUTATION_PERMUTE, gene \(i\) will be swapped with a
randomly selected gene. If PGASetMutationType() is set to
PGA_MUTATION_CONSTANT, a constant integer value (by default
one) will be added (subtracted) to (from) the existing allele value. The
constant value may be set to 34, for example, with
PGASetMutationIntegerValue() with parameters (ctx, 34).
Three of the real-valued mutation operators are of the form
\(v \leftarrow v \pm p \times v\), where \(v\) is the existing
allele value. They vary by how \(p\) is selected. First, if
PGASetMutationType() is set to PGA_MUTATION_CONSTANT,
\(p\) is the constant value 0.01. It may be set to .02, for
example, with PGASetMutationRealValue() with parameters
(ctx, .02). Second, if PGASetMutationType()
is set to PGA_MUTATION_UNIFORM, \(p\) is selected
uniformly from the interval \((0,.1)\). To select \(p\)
uniformly from the interval \((0,1)\) call
PGASetMutationRealValue() with parameters (ctx, 1). Third,
if PGASetMutationType() is set to PGA_MUTATION_GAUSSIAN,
\(p\) is selected from a Gaussian distribution (this is the default
real-valued mutation operator) with mean 0 and standard deviation 0.1.
To select \(p\) from a Gaussian distribution with mean 0 and
standard deviation 0.5 call PGASetMutationRealValue() with
parameters (ctx, .5). Finally, if PGASetMutationType() is
set to PGA_MUTATION_RANGE, gene \(i\) will be replaced
with a value selected uniformly random from the initialization range of
that gene.
For integer and real genes there is a polynomial mutation operator
selected with the mutation type constant PGA_MUTATION_POLY
[DG96]. It works by drawing a random number from a
polynomial probabilty density function for a fixed mutation interval.
The mutation interval by default is between the current allele value and
the lower/upper initialisation range of the gene. Unless you also call
PGASetMutationBoundedFlag() or PGASetMutationBounceBackFlag()
to keep mutation within the bounds of the initialization range, the
default value does not make much sense (because the current value may
already exceed the boundary). In that case (and other cases where you
want a fixed mutation range) you can call PGASetMutationPolyValue() to
set the mutation range. The polynomial mutation distribution has a
parameter \(\eta_m\) that specifies how likely values far away from
the current allele are selected, the higher this value gets, the nearer
the mutated values stays to the parent. You can set this parameter with
PGASetMutationPolyEta(), the default is 100 [DD14].
For Differential Evolution (DE), the strategy is implemented as the
mutation type PGA_MUTATION_DE. Note that for the full
DE algorithm not just a special mutation type is needed, see
section Differential Evolution for an introduction. You
typically want to chose mutation only, linear selection, and
pairwise-best replacement. For DE, real- and integer-valued genes are
typically called vectors (because a gene is a vector of real- or
integeer-valued alleles), we use that term in the following.
The default strategy of DE is to compute the distance of a pair of random vectors in the population and add this difference to a randomly-chosen third vector:
Where \(g\) denotes the generation, \(i\) is the running
population index, and \(r_0\), \(r_1\), and \(r_2\) are
random population indeces different from each other and the running
index \(i\). The factor \(F\), called the scale factor, is a
parameter of the search and can be specified with
PGASetDEScaleFactor(), the default is 0.9. The range for this
parameter is \([0,2]\) but typical values are in the range
\([0.3,1)\), the exact value \(1.0\) should not be chosen
because it reduces the number of mutants and thus potentially the
genetic variance [PSL05].
The resulting mutant vector \(V_i\), also called the donor vector,
is then combined via crossover with the member \(i\) of the population,
\(X_i\). Note that the crossover in this implementation of DE is
not the normal genetic algorithm crossover (from
section Crossover), in fact when using DE, crossover is
typically turned off by setting PGASetMixingType() to
PGA_MIX_MUTATE_ONLY. Instead DE uses its own crossover
implementation within the PGA_MUTATION_DE mutation implementation.
For each vector element (allele), a random variable with a crossover
probability specified by PGASetDECrossoverProb() (default 0.9) is
chosen. In the default binomial crossover variant of DE this variable
selects an element from either the donor vector \(V_i\) or
\(X_i\). In the DE literature this parameter is typically called
Cr. At least one random element from \(V_i\) is always selected,
so with a crossover probability of 0, exactly one element from the donor
vector is selected. With a crossover probability of 1, all elements
from the donor vector are selected. Crossover plays a significat role in
optimisation. For decomposable problems (where each dimension of the
problem can be optimized separately [Sal96]) a low crossover rate
\(0 \le Cr \le 0.2\) is a good choice. For non-decomposable problem
a high crossover rate should be chosen, i.e. \(0.9 \le Cr \le 1\)
[PSL05].
The resulting individual after crossover is placed in the new population. If pairwise-best population replacement is selected (the default in the DE literature, see section Population Replacement) it is later compared with the old individual \(X_i\) in the old population which it replaces if it has better fitness.
There are different variants of DE and a notation was established to distinguish these variants. The notation uses a 4-tuple where each element is delimited with a ’/’. The first element in the tuple is always the string DE for Differential Evolution. The second element describes the variant. The most common (often called the classic variant) selects a random element from the population for modification and is therefore called rand, see equation (1). The third tuple-element is the number of difference-pairs applied to the modified element, it is typically one or two. If we use two differences, the formula in equation (1) would become:
The number of differences can be specified with PGASetDENumDiffs() and
defaults to 1. Note that not all DE strategies use this parameter.
The fourth final element specifies the crossover strategy. For the
default DE-crossover strategy following a binomial distribution (in
standard GA terms this type of crossover is often called uniform
crossover) this final element is termed bin. The crossover for DE can
be set with PGASetDECrossoverType(). The default is binomial
crossover, exponential crossover can be set, see constants in group
Differential Evolution Crossover Constants. So for the default DE strategy the name is
DE/rand/1/bin with the exponential crossover selected, we would get
DE/rand/1/exp. Binomial crossover tosses a biased coin with
probability \(Cr\) for each allele. If the coin turns out ’1’, the
allele is taken from the donor vector, otherwise the allele from the
current individual is retained. For exponential crossover an index in
the gene is randomly selected and taken from the donor vector. For all
subsequent alleles (starting at the randomly selected index) a coin is
tossed. As long as the coin is ’1’, the allele is taken from the donor
vector. The first time the coin-toss doesn’t yield a ’1’, all the
remaining alleles are taken retained from the original individual. This
is a form of two-point crossover like in other types of genetic
algorithms but with a different distribution. The binomial crossover is
beneficial if the allele positions in the problem are uncorrelated. If
there is a corellation between allele positions, exponential crossover
may be beneficial [TF14].
The DE variant (the second tuple element) can be selected with
PGASetDEVariant() and defaults to PGA_DE_VARIANT_RAND.
The different variants are documented in group
Constants for Differential Evolution Variants. Another variant is the best variant
which uses the current best individual for modification according to
equation (3). This variant is selected with the contant
PGA_DE_VARIANT_BEST.
A third variant called either-or [PSL05] is
selected with the constant PGA_DE_VARIANT_EITHER_OR. It randomly
selects among a mutation operator and a recombination operator according
to equation (4).
The probability \(p_F\) defaults to 0.5 and can be set with
PGASetDEProbabilityEO(). The parameter \(K\) defaults to
\(0.5 \cdot (F + 1)\) [PSL05] where F is
the scale factor, it can be set with PGASetDEAuxFactor(). Note that
the either-or variant ignores the parameter specifying the number of
difference vectors (specified with PGASetDENumDiffs()). The expression
rand\(_i\)(0, 1) denotes a random number in the range
\([0, 1)\) which is re-generated for each individual \(i\).
When computing the donor vector \(V_i\), the scale factor \(F\) can be perturbed. This can either be done anew for each individual or for each allele of each individual. The first variant is called dither while the second variant is called jitter. Note that jitter not only changes the length of the difference vector but also its orientation [PSL05]. With uniform jitter we get a new factor \(F_j\), the index \(j\) denoting the allele while \(i\) is the index of the current individual [PSL05]:
The same applies for dither, but in the case of dither the factor is
either applied anew for each individual (when setting
PGASetDEDitherPerIndividual() to PGA_TRUE) or only once per
generation (the default being once per generation), note that for the
case where the dither is applied once per generation the index \(i\)
of \(K_{\text{jit}}{}\) in equation (6) would refer the
the generation:
The new \(F_j\) and/or \(F_i\) replaces \(F\) in
equations (1) to (4) and both, the default
\(K_{\text{jit}}\) and the default \(K_{\text{dit}}\) are zero
by default. If both are non-zero, both are applied. Defaults can can be
set with PGASetDEJitter() and PGASetDEDither(),
respectively. Very small amounts of uniformly distributed jitter (on the
order of 0.001) have been recommended for some problems [PSL05] like
digital filter design [PSL05]. Likewise quite large amounts of dither
(on the order of 0.5) are recommended for these problems.
Some of the integer- and real-valued mutation operators may generate
allele values outside the initialization range of that gene. By default,
the allele value will not be reset to the lower (upper) value of the
initialization range for that gene. By calling
PGASetMutationBoundedFlag() with parameters (ctx, PGA_TRUE)
the allele values will be set to the value of the bound if they fall
outside of the initialization range. It was argued that setting the
value to the bound would reduce the genetic variance and could lead to
premature convergence if several individuals get the same value [PSL05].
Therefore an alternative called “Bounce-Back” was proposed: If
PGASetMutationBounceBackFlag() is called with parameters
(ctx, PGA_TRUE), the new value is set to a random value between the
old value and the bound.
A note on the use of the DE mutation type together with other selection
or replacements schemes: The DE mutation is very disruptive. It will not
work well or not work at all with a non-elitist replacement scheme. Due
to the high disruption, if not retaining at least one best individual in
each generation, it is very likely that the search will diverge. Good
choices for an elitist strategy are the two elitist replacement schemes
PGA_POPREPL_PAIRWISE_BEST (which is the standard replacement scheme
for Differential Evolution) and PGA_POPREPL_RTR. The latter may help
if the algorithm stagnates due to premature convergence. In that case
RTR can help to retain more genetic diversity. For details see
section Population Replacement.
Restart
The restart operator reseeds a population from the best string. It does so by seeding the new population with the best string and generating the remainder of the population as mutated variants of the best string.
By default the restart operator is not invoked. Calling
PGASetRestartFlag() with parameters (ctx, PGA_TRUE) will cause
the restart operator to be invoked. By default PGAPack will restart
every 50 iterations. Calling PGASetRestartFrequencyValue()
with (ctx, 100) will restart every 100
iterations instead. When creating the new strings from the best string
an individual allele undergoes mutation with probability 0.5. This can
be changed to 0.9 by calling
PGASetRestartAlleleChangeProb() with parameter 0.9.
For binary-valued strings the bits are complemented. For integer- and
real-valued strings the amount to change is set with
PGASetMutationIntegerValue() and PGASetMutationRealValue(),
respectively. Character-valued strings are changed according to the
rules in Section Mutation for mutating character strings.
String Evaluation and Fitness
In a genetic algorithm each string is assigned a nonnegative, real-valued fitness. This is a measure, relative to the rest of the population, of how well that string satisfies a problem-specific metric. In PGAPack calculating a string’s fitness is a two-step process. First, the user supplies a real-valued evaluation (sometimes called the raw fitness) of each string. Second, this value is mapped to a fitness value.
It is the user’s responsibility to supply a function to evaluate an
individual string. As discussed in Section Required Functions,
the name of this function is specified as the second argument to
PGARun(). The calling sequence for this function (which we call
evaluate in the rest of this section, but may have any name) must
follow the format given here. In C the format is
double evaluate (PGAContext *ctx, int p, int pop, double *aux);
and in Fortran
double precision function evaluate (ctx, p, pop, aux)
integer ctx, p, pop
double precision aux(*)
The function evaluate will be called by PGARun() whenever a string
evaluation is required. p is the index of the string in population
pop that will be evaluated. The correct values of p and pop
will be passed to the evaluation function by PGARun(). (If
PGARun() is not used, PGAEvaluate() must be. See
Chapter Explicit Usage.) As shown below, p and pop are
used for reading (and sometimes writing) allele values. Sample
evaluation functions are shown in Figures PGAPack C Program for the Maxbit Example and
PGAPack Fortran Program for the Maxbit Example, and online in the ./examples
directory.
In addition to returning just one evaluation, PGAPack supports additional auxiliary evaluations. The default use for this mechanism is the specification of constraints on the objective function. If a problem does not allow all areas of the search space because it may contain invalid solutions, additional restrictions on the validity of points in the search space may be specified via constraints.
Another use-case for auxiliary evaluations is multiobjective optimization: The algorithm is not just searching for one solution but for an array of objectives that can usually not all be optimized to their optimum value. Instead a better value for one objective may necessitate a worse value for another objective. A multiobjective algorithm tries to find many non dominated solutions to a problem (a solution is said to dominate another solution if it is better in at least one objective but not worse in any other objective). These non-dominated solutions are said to lie on a Pareto Front after the mathematician Vilfredo Pareto who first defined the concept today known as pareto optimality.
PGAPack now implements multi-objective optimization with the Nondominated Sorting Genetic Algorithm (Version 2) [DPAM02] as a replacement strategy. You can mix multi-objective optimization and constraints. See below and section Population Replacement for details.
By default, auxiliary evaluations are used for constraints. All auxiliary evaluation are summed if the value is positive. If it is zero or negative, the constraint is not violated and not included in the sum. So the algorithm is minimizing constraint violations. Individuals are sorted by the amount of their constraint violations and the value of the objective function. If an individual without constraint violations is compared to one with constraint violations, the one without violations wins. For two individuals with constraint violations the one with the lower sum of violations wins. For two individuals without constraint violations the normal comparison (depending on the direction of the search, i.e. minimization or maximization) is used. This algorithm works better than trying to code the constraint violations into a complicated evaluation function. It was shown to work better than customized penalty functions by Deb [Deb00].
With this algorithm for optimizing constraints, the constraints are
optimized first, only after solutions without constraint violations have
been found is the objective function considered. This has the drawback
that for certain problems the search will end up in a region of the
search space where the constraints are not violated but where no good
solutions exist. So with some problems the solutions found are very far
from the optimum. An idea by Takahama and Sakai
[TS10], [TS06] introduces an
\(\epsilon\)-constraint mechanism. An epsilon tolerance is
introduced and initialized with the constraint violation sum of the
\(\theta\)-best individual. The index of the individual
\(\theta\) can be set with PGASetEpsilonTheta(), the default is
\(0.2\) the population size.
The comparison of evaluations is modified to include an
\(\epsilon\)-tolerance: If both individuals have a constraint
violation below the tolerance, the evaluation is compared. If only one
individual exceeds the tolerance the other individual wins and if both
exceed the tolerance, the one with the lower constraint sum wins. The
\(\epsilon\) is slowly decreased until it becomes zero at some
generation \(T_c\). The slope of decrease can be specified with the
PGASetEpsilonExponent() function, values between 2 (slow decrease) and
10 (fast decrease) are possible. The default is an adaptive algorithm
for decrease of \(\epsilon\) described in the 2010 paper
[TS10] that works well in practise.
For using the \(\epsilon\)-constraint method, the generation
\(T_c\) until which \(\epsilon\) is decreased needs to be set
using the PGASetEpsilonGeneration() function, the default is zero.
Note that PGASetEpsilonGeneration() needs to be below the value set
with PGASetMaxGAIterValue() even if the latter is not used as a
stopping criterion. Also note that the stopping criteria (see
section Stopping Criteria) are modified to not stop as
long as \(\epsilon\) is not zero.
Auxiliary evaluations are returned in an array pointed to by the aux
parameter of the users’s evaluation function. To use auxiliary
evaluations, the number of auxiliary evaluations has to be specified
with the PGASetNumAuxEval() function which gets the number of
auxiliary evaluations as the second parameter. The default is 0. If you
want to use multi-objective optimization, optionally with constraints,
you need to specify the number of constraints using the
PGASetNumConstraint() function. By default the number of constraints
is equal to the number of auxiliary evaluations. So if you want to use
multi-objective evaluation you need to set the number of constraints
lower (optionally to zero if you have only multi-objective optimization
without constraints) than the number of auxiliary evaluations.
Note that auxiliary evaluations can not be used together with selection schemes that use mechanisms where individuals are not directly compared. These currently are proportional selection and stochastic universal selection, see section Selection.
Traditionally, genetic algorithms assume fitness values are nonnegative
and monotonically increasing the more fit a string is. The user’s
evaluation of a string, however, may reflect a minimization problem
and/or be negative. Most modern selection algorithms (e.g. the default
tournament variants) directly compare individuals and will directly use
the users evaluation. There are two selection mechanisms,
PGA_SELECT_SUS and PGA_SELECT_PROPORTIONAL which need a
nonnegative and monotonically increasing fitness. Only for these the
user’s evaluation value is mapped to a nonnegative and monotonically
increasing fitness value.
You may think of the algorithm used as follows (actually for the ranking
method the evaluation value is never translated): First, all evaluations
are mapped to positive values (if any were negative). Next, these values
are translated to a maximization problem (if the direction of
optimization specified was minimization). Finally, these values are
mapped to a fitness value by using the identity (the default), linear
ranking, or linear normalization, The choice of fitness mapping may be
set with the function PGASetFitnessType(). The second argument
defines the type, these are documented in group
Constants for Fitness Types and allow the identity, linear ranking, or linear
normalization, respectively.
Note that PGA_FITNESS_RAW and PGA_FITNESS_NORMAL
are subject to overflows if you have very large (or very small negative)
fitness values. If this occurs, an error message is printed and the
program terminates. Letting the search continue with such an overflow
would map many different evaluation values to the same fitness. For
such ill-conditioned problems you should use the ranking variant
PGA_FITNESS_RANKING.
A linear rank fitness function [Bak87], [Whi89] is given by
where \(rank(p)\) is the index of string \(p\) in a list sorted
in order of decreasing evaluation function value, and \(N\) is the
population size. Ranking requires that \(1 \leq Max \leq 2\), and
\(Min + Max = 2\). The default value for \(Max\) is 1.2. It may
be set to 1.1 with PGASetMaxFitnessRank().
In linear normalization the fitness function is given by
where \(K\) and \(C\) are the constants \(\sigma \cdot N\) and \(\sigma\), where \(\sigma\) is the standard deviation of the user’s evaluation function values after they have been transformed to positive values for a maximization problem.
If the direction of optimization is minimization, the values are
remapped for maximization. Calling the function
PGASetFitnessMinType() with parameters (ctx, PGA_FITNESSMIN_CMAX)
will remap by subtracting the worst evaluation value from each
evaluation value (this is the default). The worst evaluation value is
multiplied by 1.01 before the subtraction so that the worst string has a
nonzero fitness. Calling the function PGASetFitnessCmaxValue()
with parameters (ctx, 1.2) will change the
multiplier to 1.2 Alternatively, if PGA_FITNESSMIN_RECIPROCAL
is specified the remapping is done by using the reciprocal of the
evaluation function.
Note that for algorithms that can directly compare individuals in the selection method (any of the tournament selection methods, truncation selection, and linear selection, see section Selection) or in the replacement scheme (restricted tournament replacement or pairwise best replacement, see section Population Replacement) do not use the fitness but compare the evaluation value (and optionally the sum of constraint violations) directly.
Accessing Allele Values
For each of the native data types, PGAPack provides a matched pair of
functions that allow the user to read or write (change) any allele
value. If the data type is PGA_DATATYPE_BINARY
int bit;
bit = PGAGetBinaryAllele (ctx, p, pop, i);
will assign to bit the binary value of the ith gene in string
p in population pop. To set the ith gene in string p
in population pop to 1, use
PGASetBinaryAllele (ctx, p, pop, i, 1);
If the data type is PGA_DATATYPE_INTEGER
int k;
k = PGAGetIntegerAllele (ctx, p, pop, i);
will assign to k the integer value of the ith gene in string
p in population pop. To set the ith gene in string p
in population pop to 34, use
PGASetIntegerAllele (ctx, p, pop, i, 1, 34);
If the data type is PGA_DATATYPE_REAL
double x;
x = PGAGetRealAllele (ctx, p, pop, i);
will assign to x the real value of the ith gene in string
p in population pop. To set the ith gene in string p
in population pop to 123.456, use
PGASetRealAllele (ctx, p, pop, i, 1, 123.456);
If the data type is PGA_DATATYPE_CHARACTER
char c;
c = PGAGetCharacterAllele (ctx, p, pop, i);
will assign to c the character value of the ith gene in string
p in population pop. To set the ith gene in string p
in population pop to “Z”, use
PGASetCharacterAllele (ctx, p, pop, i, 1, 'Z');
Representing an Integer with a Binary String
A binary string may be used to represent an integer by decoding the bits into an integer value. In a binary coded decimal (BCD) representation, a binary string is decoded into an integer \(k \in [0,2^{N}-1]\) according to
where \(N\) is the string length, and \(b_i\) the value of the
\(i\)th bit. For example, to decode the integer k from the ten
bits in bit positions 20–29, use
int k
k = PGAGetIntegerFromBinary (ctx, p, pop, 20, 29);
The function PGAEncodeIntegerAsBinary() will encode an integer as a
binary string. For example, to encode the integer 564 as a 12-bit binary
string 2 in the substring defined by bits 12–23, use
PGAEncodeIntegerAsBinary (ctx, p, pop, 12, 23, 564);
In a BCD representation, two numbers that are contiguous in their
decimal representations may be far from each other in their binary
representations. For example, 7 and 8 are consecutive integers, yet
their 4-bit binary representations, 0111 and 1000, differ in the
maximum number of bit positions. 3 Gray codes define a different
mapping of binary strings to integer values from that given by
Eq. (7) and may alternatively be used for
representing integer (or real, see below) values in a binary string. The
second and third columns in Table Binary and Gray Codes show how the
integers 0–7 are mapped to Eq. (7) and to the
binary reflected Gray code (the most commonly used Gray code
sequence), respectively. In the binary reflected Gray code sequence, the
binary representations of consecutive integers differ by only one bit (a
Hamming distance of one).
To decode the integer k from a binary reflected Gray code
interpretation of the binary string, use
k = PGAGetIntegerFromGrayCode (ctx, p, pop, 20, 29);
To encode 564 as a 12-bit binary string in the substring defined by bits 12–23 using a Gray code, use
PGAEncodeIntegerAsGaryCode (ctx, p, pop, 12, 23, 564);
\(k\) |
Eq. (7) Gray code |
|
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Representing a Real Value with a Binary String
A binary string may also be used to represent a real value. The decoding of a binary string to a real-value is a two-step process. First, the binary string is decoded into an integer as described in Section Representing an Integer with a Binary String. Next, the integer is mapped from the discrete interval \([0,2^{N}-1]\) to the real interval \([L,U]\) by using the formula
(and generalizing \([0,2^{N}-1]\) to \([a,b]\)). For example, to
decode the double x from the 20 bits given by the binary string
stored in bit positions 10–29 onto the interval \([-10.0,20.0]\),
use
x = PGAGetRealFromBinary (ctx, p, pop, 10, 29, -10.0, 20.0);
To encode -18.3 on the interval \([-50.0,50.0]\) using a 20-bit BCD binary string, use
PGAEncodeRealAsBinary (ctx, p, pop, 0, 19, -50.0, 50.0, -18.3);
The functions PGAGetRealFromGrayCode() and
PGAEncodeRealAsGrayCode()
provide similar functionality for Gray-coded strings.
All the functions for getting and setting allele values are documented
in function group Allele Access.
Example
As an example, suppose the user has a real-valued function \(f\) of three real variables \(x_1\), \(x_2\), and \(x_3\). Further, the variables are constrained as follows.
The user wishes to use 10 bits for the binary representation of \(x_1\) and \(x_2\), and 20 bits for the binary representation of \(x_3\) (perhaps for higher accuracy), and a Gray code encoding. This may be done as follows.
#include "pgapack.h"
double grayfunc (PGAContext *ctx, int p, int pop);
double f (double x1, double x2, double x3);
int main (int argc, char **argv)
{
PGAContext *ctx;
ctx = PGACreate (&argc, argv, PGA_DATATYPE_BINARY, 40, PGA_MINIMIZE);
PGASetUp (ctx);
PGARun (ctx, grayfunc);
PGADestroy (ctx);
return;
}
double grayfunc (PGAContext *ctx, int p, int pop)
{
double x1, x2, x3, v;
x1 = PGAGetRealFromGrayCode (ctx, p, pop, 0, 9, -10., 0.);
x2 = PGAGetRealFromGrayCode (ctx, p, pop, 10, 19, 0., 10.);
x3 = PGAGetRealFromGrayCode (ctx, p, pop, 20, 39, -10., 10.);
v = f (x1, x2, x3);
return v;
}
In Fortran, the bit indices would be 1–10, 11–20, and 21–40,
respectively. The number of bits allocated for the binary representation
determines the accuracy with which the real value can be calculated.
Note in this example the function f need not be modified; the
function grayfunc is used as a “wrapper” to get variable values out
of the GA and return the value calculated by f.
Report Options
Calling PGASetPrintFrequencyValue() with parameters (ctx, 40)
will print population statistics
every 40 iterations. The default is every ten iterations. The best
evaluation is always printed. To print additional statistics, set the
second argument of the function PGASetPrintOptions() to
one of the values documented in group Constants for Reporting
to print the online analysis, offline analysis,
worst evaluation, average evaluation, genetic distance, or string
itself, respectively. PGASetPrintOptions() may be called multiple
times to specify multiple print options.
Utility Functions
Random Numbers
By default, PGAPack will seed its random number generator by using a
value from the system clock. Therefore, each time PGAPack is run, a
unique sequence of random numbers will be used. For debugging or
reproducibility purposes, however, the user may wish to use the same
sequence of random numbers each time. This may be done using the
function PGASetRandomSeed() to initialize the random number generator
with the same seed each time, for example,
PGASetRandomSeed (ctx, 1);
PGARandom01() with second parameter 0 will return a random
number generated uniformly on \([0,1]\). If the second argument is
not :math`0`, it will be used to reseed the random number sequence.
PGARandomFlip() flips a biased
coin. For example,
PGARandomFlip (ctx, .7)
will return PGA_TRUE approximately 70% of the time. Calling
PGARandomInterval() with parameters (ctx, -10, 30) will
return an integer value generated uniformly on \([-10,30]\).
PGARandomUniform() with parameters (ctx, -50., 50.) will
return a real value generated uniformly randomly on the interval
\([-50,50]\). PGARandomGaussian() with parameters
(ctx, 0., 1.) will return a real value generated from a Gaussian
distribution with mean zero and standard deviation one.
Print Functions
Calling PGAPrintPopulation() with parameters (ctx, stdout, pop)
will print the evaluation function value, fitness value, and string for
each member of population pop to stdout. This function may not
be called until after PGASetUp() has been called.
PGAPrintContextVariable() with parameters (ctx, stdout)
will print the value of all fields in the context variable to
stdout. PGAPrintIndividual() with parameters
(ctx, stdout, p, pop) will print the evaluation function value,
fitness value, and string of individual p in population pop to
stdout. PGAPrintString() with parameters
(ctx, stdout, p, pop) will print the string of individual
p in population pop to stdout.
PGAPrintVersionNumber() will print the PGAPack version number.
Miscellaneous
PGAGetGAIterValue() will return the current iteration of the GA
and PGAGetEvalCount() returns the number of evaluation function
calls so far.
PGAGetBestIndex() (PGAGetWorstIndex()) will return the
index of the most (least) fit member of population pop.
PGAUpdateOffline() (PGAUpdateOnline()) will update the
offline (online) analysis based on the new generation’s results.
PGAGeneDistance() returns a double, which is the average
genetic distance between the strings in population pop. The function
call
PGAError (ctx, "popindex=", PGA_FATAL, PGA_INT, (void *)&popindex)
will print the message “popindex=-1” (assuming the value of popindex
is -1) and then exit PGAPack. If the third argument had been
PGA_WARNING instead, execution would have continued, see group
Constants for Error Printing Flags. In addition to PGA_INT, valid data
types are documented in group Constants for Error Printing. There is
also a printf-style error printing function PGAErrorPrintf().
Command-Line Arguments
PGAPack provides several command-line arguments. These are only
available to C programs, although in some cases both C and Fortran
programs can achieve the equivalent functionality with function calls.
For example, PGAUsage() provides the same functionality as the
-pgahelp command line option. See Chapter Debugging Tools for the
function call equivalents.
-pgahelp get this message
-pgahelp debug list of debug options
-pgadbg <level> set debug option
-pgadebug <level> set debug option
-pgaversion Print current PGAPack version number, parallel or
sequential, and debug or optimized
Explicit Usage
This chapter discusses how the user may obtain greater control over the
steps of the GA by not using the PGARun() command, but instead
calling the data-structure-neutral functions directly. One ramification
of this is that the PGARun() interface no longer masks some of the
differences between parallel and sequential execution. The examples in
this chapter are written for sequential execution only.
Chapter Parallel Aspects shows how they may be executed in
parallel.
Notation
To understand the calling sequences of the functions discussed in this chapter, one must know of the existence of certain data structures and the user interface for accessing them. It is not necessary to know how these data structures are implemented, since that is hidden by the user interface to PGAPack.
PGAPack maintains two populations: an old one and a new one. The
size of each population is the value returned by PGAGetPopSize(). In
addition, each population contains two temporary working locations. The
string length is the value specified to PGACreate() and returned by
PGAGetStringLength().
Formally, string \(p\) in population \(pop\) is referred to by
the 2-tuple (p, pop) and the value of gene \(i\) in that string
by the 3-tuple (i, p, pop). In PGAPack, pop must be one of the
two symbolic constants PGA_OLDPOP or PGA_NEWPOP to
refer to the old or new population, respectively. At the end of each GA
iteration, the function PGAUpdateGeneration() makes sure these
symbolic constants are remapped to the correct population. The string
index p must be either an integer between 0 and \(P-1\) (or 1
and \(P\) in Fortran) or one of the symbolic constants
PGA_TEMP1 or PGA_TEMP2, to reference one of the
two temporary locations, respectively.
Simple Sequential Example
The example in Figure Simple Example of Explicit Usage is a
complete PGAPack program that does not use PGARun(). It is an
alternative way to write the main program for the Maxbit example of
Section Maxbit Problem in C. We refer to it as a simple
example because it uses PGARunMutationAndCrossover() to encapsulate
the recombination step. The PGACreate() and PGASetUp() functions
were discussed in the last chapter. PGASetUp() creates and randomly
initializes the initial population. This population, referred to
initially by the symbolic constant PGA_OLDPOP, is evaluated by the
PGAEvaluate() function. The third argument to PGAEvaluate()
is the name of the user’s evaluation function. The function prototype
for evaluate must be as shown in Figure Simple Example of Explicit Usage
and discussed earlier in Sections Required Functions and
String Evaluation and Fitness. The PGAFitness() function maps the user’s
evaluation function values into fitness values.
The while loop runs the genetic algorithm. PGADone() returns
PGA_TRUE if any of the specified stopping criteria have been met,
otherwise PGA_FALSE. PGASelect() performs selection
on population PGA_OLDPOP. PGARunMutationAndCrossover()
uses the selected strings to create the new population by applying the
crossover and mutation operators. PGAEvaluate() and
PGAFitness() evaluate and map to fitness values the newly
created population. PGAUpdateGeneration() updates the GA
iteration count and resets several important internal arrays (don’t
forget to call it!). PGAPrintReport() writes out genetic
algorithm statistics according to the report options specified. Note
that the argument to PGAPrintReport() is the old population,
since after PGAUpdateGeneration() is called, the newly created
population is in PGA_OLDPOP. Finally, PGADestroy()
releases any memory allocated by PGAPack when execution is complete.
The functions PGADone(), PGAUpdateGeneration(), and
PGAEvaluate() take an MPI communicator (see
Appendix Parallelism Background and Chapter Parallel Aspects) as
an argument. For sequential execution the value NULL should be
specified for this argument. A parallel, or sequential and parallel,
version of this example is given in Section Explicit Use.
#include "pgapack.h"
double evaluate (PGAContext *ctx, int p, int pop, double *aux);
int main (int argc, char **argv)
{
PGAContext *ctx;
ctx = PGACreate (&argc, argv, PGA_DATATYPE_BINARY, 100, PGA_MAXIMIZE);
PGASetUp (ctx);
PGAEvaluate (ctx, PGA_OLDPOP, evaluate, NULL);
PGAFitness (ctx, PGA_OLDPOP);
while (!PGADone(ctx, NULL)) {
PGASelect (ctx, PGA_OLDPOP);
PGARunMutationAndCrossover (ctx, PGA_OLDPOP, PGA_NEWPOP);
PGAEvaluate (ctx, PGA_NEWPOP, evaluate, NULL);
PGAFitness (ctx, PGA_NEWPOP);
PGAUpdateGeneration (ctx, NULL);
PGAPrintReport (ctx, stdout, PGA_OLDPOP);
}
PGADestroy (ctx);
return 0;
}
Complex Example
#include "pgapack.h"
double evaluate (PGAContext *ctx, int p, int pop, double *aux);
int main (int argc, char **argv)
{
PGAContext *ctx;
int i, j, n, m1, m2, popsize, numreplace;
double probcross;
ctx = PGACreate (&argc, argv, PGA_DATATYPE_BINARY, 100, PGA_MAXIMIZE);
PGASetUp (ctx);
probcross = PGAGetCrossoverProb (ctx);
popsize = PGAGetPopSize (ctx);
numreplace = PGAGetNumReplaceValue (ctx);
PGAEvaluate (ctx, PGA_OLDPOP, evaluate, NULL);
PGAFitness (ctx, PGA_OLDPOP );
while (!PGADone (ctx, NULL)) {
PGASelect (ctx, PGA_OLDPOP);
PGASortPop (ctx, PGA_OLDPOP);
n = popsize - numreplace;
for ( i=0; i < n; i++ ) {
j = PGAGetSortedPopIndex (ctx, i);
PGACopyIndividual (ctx, j, PGA_OLDPOP, i, PGA_NEWPOP);
}
while (n < popsize) {
m1 = PGASelectNextIndex (ctx, PGA_OLDPOP);
m2 = PGASelectNextIndex (ctx, PGA_OLDPOP);
if (PGARandomFlip (ctx, probcross)) {
PGACrossover (ctx, m1, m2, PGA_OLDPOP, PGA_TEMP1, PGA_TEMP2, PGA_NEWPOP);
PGAMutate (ctx, PGA_TEMP1, PGA_NEWPOP);
PGAMutate (ctx, PGA_TEMP2, PGA_NEWPOP);
PGACopyIndividual (ctx, PGA_TEMP1, PGA_NEWPOP, n, PGA_NEWPOP);
PGACopyIndividual (ctx, PGA_TEMP2, PGA_NEWPOP, n+1, PGA_NEWPOP);
n += 2;
}
else {
PGACopyIndividual (ctx, m1, PGA_OLDPOP, n, PGA_NEWPOP);
PGACopyIndividual (ctx, m2, PGA_OLDPOP, n+1, PGA_NEWPOP);
n += 2;
}
}
PGAEvaluate (ctx, PGA_NEWPOP, evaluate, NULL);
PGAFitness (ctx, PGA_NEWPOP);
PGAPrintReport (ctx, stdout, PGA_NEWPOP);
PGAUpdateGeneration (ctx, NULL);
}
PGADestroy (ctx);
return 0;
}
The primary difference between the “complex” example in
Figure Example of Explicit Usage and the “simple” example
in Figure Simple Example of Explicit Usage is that the steps
encapsulated by PGARunMutationAndCrossover() have been written out
explicitly. The function PGASortPop() sorts a population according to
the criteria specified by PGASetPopReplaceType()
(Section Population Replacement). The sorted indices are
accessed via PGAGetSortedPopIndex(). In the example, the five lines
that follow PGASortPop() copy the strings that are not created by
recombination from the old population to the new population.
The while loop that follows creates the remainder of the new
population. PGASelectNextIndex() returns the indices of the strings
selected by PGASelect(). PGARandomFlip() flips a coin
biased by the crossover probability to determine whether the selected
strings should undergo crossover and mutation or should be copied
directly into the new population. PGACrossover uses the parent
strings m1 and m2 from population PGA_OLDPOP to create two
child strings in the temporary locations PGA_TEMP1 and
PGA_TEMP2 in PGA_NEWPOP population.
PGAMutate() mutates the child strings and PGACopyIndividual(),
then copies them into the new population. If the strings do not undergo
crossover and mutation, they are copied into the new population
unchanged. The rest of the steps are the same as those in
Figure Simple Example of Explicit Usage, except that for illustrative
purposes we call PGAPrintReport() before
PGAUpdateGeneration(). In that case we use population
PGA_NEWPOP as the population pointer.
Explicit PGAPack Functions
This section briefly discusses other functions not shown in the previous
examples or discussed in Chapter Basic Usage. Additional
information about these and other PGAPack functions is contained in
Appendix Function Bindings (function bindings) and the
./examples directory.
PGARunMutationAndCrossover() and PGARunMutationOrCrossover()
perform the recombination step. The former applies mutation to strings
that undergo crossover. The latter applies only mutation to strings that
did not undergo crossover. Note that this means that when
PGARunMutationAndCrossover() is selected, strings that are not
crossed over (because the random process did not select the individuals
for crossover with the given crossover probability) will also not be
mutated! If no crossover is wanted, PGARunMutationOnly() can be
used for mutation only without crossover.
The restart operator described earlier in Section Restart
can be invoked explicitly by calling PGARestart() with
parameters (ctx, oldpop, newpop), where the best string from
population oldpop is used to initialize population newpop.
The function PGADuplicate() with parameters
(ctx, p, PGA_NEWPOP, PGA_NEWPOP) returns PGA_TRUE if
string p in population PGA_NEWPOP is a duplicate of any of the
strings in population PGA_NEWPOP which were inserted into the hash
table using PGAHashIndividual(). Note that this function is defined
only for population PGA_NEWPOP.
Calling PGAHashIndividual() with parameters (ctx, p, PGA_NEWPOP)
hashes individual p in population PGA_NEWPOP for duplicate
checking.
Function PGAChange() with parameters (ctx, p, PGA_OLDPOP)
repeatedly applies the mutation operator to string p in population
PGA_OLDPOP until at least one mutation has occurred.
All functions related to duplicate checking do nothing if duplicate
checking has not been enabled with PGASetNoDuplicatesFlag(), the
function PGAGetNoDuplicatesFlag() can be used for checking if
duplicate checking is enabled.
In PGAPack three values are associated with each string: (1) the user’s
evaluation function value, (2) a Boolean flag to indicate whether the
evaluation function value is up to date with respect to the actual
string, and (3) the fitness value. If PGARun() is not used, the
user must manage these values explicitly.
Calling PGAEvaluate() with parameters
(ctx, PGA_NEWPOP, evaluate, comm) will execute the user’s
evaluation function, evaluate, on each string in population
PGA_NEWPOP that has changed (for example, from crossover) since its
last evaluation. PGAEvaluate() will set both the evaluation function
value and associated Boolean flag automatically. The argument comm
is an MPI communicator. Valid values are NULL for an explicitly
sequential example, or any valid MPI communicator. Depending on the
number of processes specified when the program was invoked, and the
value of the comm argument, PGAEvaluate() may be run with one or
more processes. See Chapter Parallel Aspects for further
discussion.
PGAFitness() will calculate the population fitness values from the
evaluation function values. It is an error to call PGAFitness() if
all the evaluation function values are not up to date.
These same three values may be read also. PGAGetEvaluation()
returns the evaluation function value.
PGAGetEvaluationUpToDateFlag() returns PGA_TRUE or
PGA_FALSE to indicate whether the evaluation is up to date with the
actual string or not, respectively. If PGAPack was compiled for
debugging, PGAGetEvaluation() will print a warning message if
the evaluation is not up to date. PGAGetFitness() returns the
fitness value.
At times, (e.g., applying a hill-climbing function) the user may need to
explicitly set the evaluation function value and associated Boolean flag
(fitness values can be calculated only by calling PGAFitness()).
PGASetEvaluation() with parameters (ctx, p, PGA_OLDPOP, 123.4)
will set the evaluation function value to 123.4 and the associated
Boolean flag to PGA_TRUE. The Boolean flag may be set independently
with PGASetEvaluationUpToDateFlag(). For example,
PGASetEvaluationUpToDateFlag() with parameters
(ctx, p, PGA_OLDPOP, PGA_FALSE) sets the status of the Boolean flag
of string p in population PGA_OLDPOP to out of date.
PGAMean() with parameters (ctx, a, n) returns the mean of
the n values in array a. PGAStddev() with parameters
(ctx, a, n, mean) returns the standard deviation of
the n values in array a whose mean is mean. PGARank()
with parameters (ctx, p, order, n) returns an index that is the rank
of string p as given by the sorted array order of length n.
PGAGetPrintFrequency() returns the frequency with which GA
statistics are reported. PGAGetWorstIndex() with parameters
(ctx, PGA_OLDPOP) returns the index of the string in population
PGA_OLDPOP with the worst evaluation function value.
PGAGetBestIndex() with parameters (ctx, PGA_OLDPOP) returns
the index of the string in population PGA_OLDPOP with the best
evaluation function value.
Custom Usage: Native Data Types
This chapter discusses how PGAPack may be extended by replacing some of the standard PGAPack functions with user-defined functions for use with one of PGAPack’s four native data types. This can be done from both C and Fortran.
Basics
Initialization |
|
Crossover |
|
Mutation |
|
Duplicate Checking |
|
Hashing |
|
String Printing |
|
Termination Criteria |
|
End of generation |
|
Genetic distance |
|
Pre-Evaluate Hook |
In PGAPack, high-level (data-structure-neutral) functions call data-structure-specific functions that correspond to the data type used. The implementation uses function pointers that, by default, are set to the correct values for the datatype used. The user may change these defaults and set the function pointers to execute their functions instead. The functions the user can substitute for are initialization, crossover, mutation, checking for duplicate strings, string printing, termination criteria, a generic function called at the end of each GA iteration, and another generic function called before evaluation but after mutation and crossover.
The function call
PGASetUserFunction() with parameters
(ctx, PGA_USERFUNCTION_MUTATION, mymute) will
cause PGAPack to execute the function mymute whenever the mutation
operator is called. Table Customizeable Functions: Native Data Types is a list of
functions that can be customized for use with a native datatype. The
first column describes the functionality, and the second column the
symbolic constant for use with PGASetUserFunction(). The calling
sequence for these functions is fixed and must follow the function
prototypes in Table Calling Sequences for Customizable Functions. The files
./examples/templates/uf_native.c and
./examples/templates/uf_native.f contain template routines for these
functions. A specific example is given below.
Checking the termination criteria requires some discussion. The function
PGADone() will either check to see if the standard stopping criteria
(see Section Stopping Criteria) have been met, or call
the user function specified by PGA_USERFUNCTION_STOPCOND. If you
wish to have the user function check for the standard stopping criteria
in addition to whatever else it does, it should call
PGACheckStoppingConditions(). Do not call PGADone() as this
will cause an infinite loop to occur. Note that in a parallel program
PGACheckStoppingConditions() should only be called by the rank-0
process (see Chapter Parallel Aspects).
The end of generation function (which is null by default) may be used
for gathering statistics about the GA, displaying custom output,
or even call a hill-climber, etc. This function is called after all
generational computation is complete, but before the population pointers
(PGA_NEWPOP, PGA_OLDPOP) have been switched and
the standard PGAPack output printed. Therefore, be sure to use
PGA_NEWPOP as the population pointer. There is no mechanism
for suppressing the standard PGAPack generational output.
The genetic distance function computes the genetic distance
of two individuals. It is used, e.g., when restricted tournament
selection or negative assortative mating is
in use. In addition it is used when reporting of genetic distance is
selected by calling PGASetPrintOptions() with
PGA_REPORT_GENE_DISTANCE. There are implementations for the standard
data types: For binary alleles it uses the hamming distance. For real-
and integer valued genes it uses an allele-by-allele absolute value of
the difference by default (also know as Manhattan distance), i.e.
where \(s\) is the string length, \(a_{ij}\) and \(a_{ik}\) are the alleles to be compared. For character alleles it counts the number of differences. You can set the distance function for integer and real data types to an Euclidian distance by calling, e.g., for the real data type:
PGASetUserFunction (ctx, PGARealEuclidianDistance);
or for the integer data type:
PGASetUserFunction (ctx, PGAIntegerEuclidianDistance);
This will use the Euclidian distance:
When using user-defined data types together with restricted tournament selection, an implementation of the distance function for the user-defined data type has to be provided.
The Pre-Evaluate Hook function can be used for performing actions that need to be done before evaluating the generated individuals after crossover and mutation. It can be used, e.g., for repairing genes after crossover and mutation before evaluating them. It can also be used in concert with the end of generation function to perform caching of evaluations: The end of generation function would cache genes and their evaluation while the pre evaluate hook would look up newly-generated individuals in the cache: If a newly-generated individual is found in the cache, an evaluation can be saved which can have a huge impact on the runtime if evaluation is costly. Note that the probability of cache hits may be higher for binary and integer alleles than for real alleles. Note that for non-parallel implementations, caching could also be implemented in the evaluate function but for parallel implementations this would not work because each parallel instance would use a separate cache. The pre evaluation user function is called only in the rank-0 instance for a parallel implementation.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Example Problem: C
The example problem in
Figure PGAPack C Example Using Custom Mutation Operator is to
maximize \(\sum_{j=1}^{L} x_{j}\) with \(1 \leq x_j \leq L\),
where \(L\) is the string length. The optimal solution to this
problem, \(L^2\), is achieved by setting each \(x_j\) to
\(L\). The files for this example, ./examples/maxint.c and
./examples/maxint.f, contain template routines for these functions.
The example shows the use of a custom mutation function with an integer
data type. The function PGASetUserFunction() specifies that this
function, MyMutation, will be called when the mutation operator is
applied, rather than the default mutation operator. MyMutation
generates a random integer on the interval \([1,L]\).
#include <pgapack.h>
double evaluate (PGAContext *ctx, int p, int pop, double *aux);
int myMutation (PGAContext *ctx, int p, int pop, double pm);
int main (int argc, char **argv)
{
PGAContext *ctx;
int i, maxiter;
ctx = PGACreate (&argc, argv, PGA_DATATYPE_INTEGER, 10, PGA_MAXIMIZE);
PGASetUserFunction (ctx, PGA_USERFUNCTION_MUTATION, myMutation);
PGASetIntegerInitPermute (ctx, 1, 10);
PGASetUp (ctx);
PGARun (ctx, evaluate);
PGADestroy (ctx);
return 0;
}
int myMutation (PGAContext *ctx, int p, int pop, double pm)
{
int stringlen, i, k, count = 0;
stringlen = PGAGetStringLength (ctx);
for (i = 0; i < stringlen; i++)
if (PGARandomFlip (ctx, pm)) {
k = PGARandomInterval (ctx, 1, stringlen);
PGASetIntegerAllele (ctx, p, pop, i, k);
count++;
}
return (double) count;
}
double evaluate (PGAContext *ctx, int p, int pop, double *aux)
{
int stringlen, i, sum = 0;
stringlen = PGAGetStringLength (ctx);
for (i = 0; i < stringlen; i++)
sum += PGAGetIntegerAllele (ctx, p, pop, i);
return (double)sum;
}
Example Problem: Fortran
Figure PGAPack Fortran Example Using Custom Mutation Operator is the same example as in Figure PGAPack C Example Using Custom Mutation Operator written in Fortran.
include 'pgapackf.h'
include 'mpif.h'
double precision evaluate
integer myMutation
external evaluate, myMutation
integer ctx, i, maxiter, ierror
call MPI_Init (ierror)
ctx = PGACreate (PGA_DATATYPE_INTEGER, 10, PGA_MAXIMIZE)
call PGASetUserFunction (ctx, PGA_USERFUNCTION_MUTATION, & myMutation)
call PGASetIntegerInitPermute(ctx, 1, 10);
call PGASetUp (ctx);
call PGARun (ctx, evaluate);
call PGADestroy (ctx);
call MPI_Finalize(ierror)
stop
end
integer function myMutation(ctx, p, pop, pm)
include 'pgapackf.h'
integer ctx, p, pop
double precision pm
integer stringlen, i, k, count
count = 0
stringlen = PGAGetStringLength(ctx)
do i=0, stringlen
if (PGARandomFlip(ctx, pm) .eq. PGA_TRUE) then
k = PGARandomInterval(ctx, 1, stringlen)
call PGASetIntegerAllele(ctx, p, pop, i, k)
count = count + 1
endif
enddo
myMutation = count
return
end
double precision function evaluate(ctx, p, pop)
include 'pgapackf.h'
integer ctx, p, pop
integer stringlen, i, sum
sum = 0
stringlen = PGAGetStringLength(ctx)
do i=0, stringlen
sum = sum + PGAGetIntegerAllele(ctx, p, pop, i)
enddo
evaluate = sum
return
end
Custom Usage: New Data Types
This chapter discusses how PGAPack may be extended by defining a new data type. Defining a new data type may be done only in C programs.
Basics
Memory allocation |
|
Memory free |
|
String packing |
|
Mutation |
|
Crossover |
|
String printing |
|
String copying |
|
Duplicate checking |
|
Hashing |
Serialization |
|
Free serialization |
|
Deserialization |
To create a new data type, you must (1) specify PGA_DATATYPE_USER
for the datatype in the PGACreate() call and (2) for each entry in
Table Functions Required for New Data Types, call PGASetUserFunction() to
specify the function that will perform the given operation on the new
data type. If the data type is PGA_DATATYPE_USER, the string length
specified to PGACreate() can be whatever the user desires. It will be
returned by PGAGetStringLength() but is not otherwise used in the
data-structure-neutral functions of PGAPack.
When specifying a user function for string creation (with
PGA_USERFUNCTION_CREATESTRING, by default the string is freed using
the free function. If memory allocation uses different mechanisms, a
user function for freeing a chromosome can be specified with
PGA_USERFUNCTION_CHROM_FREE.
Instead of specifying a user function for building an MPI data type,
you can instead specify user functions for a serialization API
summarized in table Serialization API. The user
function for serialization PGA_USERFUNCTION_SERIALIZE is used on the
sending side. The function for deserialization
PGA_USERFUNCTION_DESERIALIZE is used at the receiving side. With the
serialization API it is possible to send/receive variable-length data
types. The serialization must reserve memory for the serialized
representation. If it uses memory allocation with malloc, the
default is to call free when the serialized value is no longer
needed. If a memory allocation system not compatible with free is
used, the user function PGA_USERFUNCTION_SERIALIZE_FREE must be
defined. When using the serialization API a user function
PGA_USERFUNCTION_BUILDDATATYPE must not be defined.
The calling sequences for the functions in
Table Functions Required for New Data Types are given in
Table Calling Sequences for New Data Type Functions. Template routines for these
functions are in the file ./examples/templates/uf_new.c.
The functions PGA_USERFUNCTION_DUPLICATE and
PGA_USERFUNCTION_HASH for user defined data types are needed
only when duplicate checking is enabled with
PGASetNoDuplicatesFlag(). Note that for duplicate checking to
work, usually both, the hashing and the duplicate function need to be
defined. An example is given in examples/c/namefull.c for C and
examples/fortran/namefull.f for Fortran. These define a hash
function and a duplicate check (comparison) function that treat all
non-matching characters alike. When implementing a hash function for
user defined datatypes the function PGAUtilHash() in
source/utility.c can be used.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
While PGAPack requires that the user supply all the functions in Table Functions Required for New Data Types, your program may not require the functionality of all of them. For example, the user really does not need to write a function to pack the strings for message-passing unless a parallel version of PGAPack is being used. In these cases, we suggest that the user supply a stub function; i.e., a function with the correct calling sequence but no functionality.
Example Problem
#include <pgapack.h>
double energy (double *, int *);
double Evaluate (PGAContext *, int, int);
void CreateString (PGAContext *, int, int, int);
int Mutation (PGAContext *, int, int, double);
void Crossover (PGAContext *, int, int, int, int, int, int);
void WriteString (PGAContext *, FILE *, int, int);
void CopyString (PGAContext *, int, int, int, int);
int DuplicateString (PGAContext *, int, int, int, int);
MPI_Datatype BuildDT (PGAContext *, int, int);
typedef struct {
double t[6]; /* ligand translation and rotation */
int sc[40]; /* ligand sidechain rotations */
} ligand;
int main (int argc, char **argv) {
PGAContext *ctx;
int maxiter;
ctx = PGACreate (&argc, argv, PGA_DATATYPE_USER, 46, PGA_MINIMIZE);
PGASetRandomSeed (ctx, 1);
PGASetMaxGAIterValue (ctx, 5000);
PGASetUserFunction (ctx, PGA_USERFUNCTION_CREATESTRING, CreateString);
PGASetUserFunction (ctx, PGA_USERFUNCTION_MUTATION, Mutation);
PGASetUserFunction (ctx, PGA_USERFUNCTION_CROSSOVER, Crossover);
PGASetUserFunction (ctx, PGA_USERFUNCTION_PRINTSTRING, WriteString);
PGASetUserFunction (ctx, PGA_USERFUNCTION_COPYSTRING, CopyString);
PGASetUserFunction (ctx, PGA_USERFUNCTION_DUPLICATE, DuplicateString);
PGASetUserFunction (ctx, PGA_USERFUNCTION_BUILDDATATYPE, BuildDT);
PGASetUp (ctx);
PGARun (ctx, Evaluate);
PGADestroy (ctx);
return 0;
}
This example illustrates use of a user-defined structure as the new data
type. The problem is one of molecular docking where one protein molecule
(the ligand) is to be docked into a second, target protein molecule.
Figure Main Program for Structure Data Type
contains the function prototypes for each function that will operate on
the new datatype, the definition of the user’s structure ligand,
and the main program.
The first three doubles of the array t in structure ligand
represent the translation of the ligand molecule in the \(x\)-,
\(y\)-, and \(z\)-axes, respectively. The last three doubles
in the array t represent the rotation of the ligand molecule about
each of the axes. The ints in the sc array represent side
chain rotations (which are discrete) of the ligand molecule.
void CreateString (PGAContext *ctx, int p, int pop, int InitFlag) {
int i;
ligand *ligand_ptr;
PGAIndividual *new;
new = PGAGetIndividual (ctx, p, pop);
if (!(new->chrom = malloc (sizeof (ligand)))) {
fprintf (stderr, "No room for new->chrom");
exit (1);
}
ligand_ptr = (ligand *)new->chrom;
if (InitFlag) {
for (i = 0; i < 3; i++)
ligand_ptr->t[i] = PGARandom01 (ctx, 0) * 20.0 - 10.0;
for (i = 3; i < 6; i++)
ligand_ptr->t[i] = PGARandom01 (ctx, 0) * 6.28 - 3.14;
for (i = 0; i < 40; i++)
ligand_ptr->sc[i] = PGARandomInterval (ctx, -20, 20);
} else {
for (i = 0; i < 6; i++)
ligand_ptr->t[i] = 0.0;
for (i = 0; i < 40; i++)
ligand_ptr->sc[i] = 0;
}
}
Figure Creation and Initialization Function for Structure Data Type
contains the function CreateString that allocates and initializes
the ligand structure. At this level of usage it is no longer always
possible to maintain the (p, pop) abstraction to specify an
individual (a string and associated fields). CreateString works
directly with the string pointer that (p, pop) is mapped to. If
InitFlag is true, CreateString will initialize the fields;
otherwise they are set to 0.
PGAGetIndividual() with parameters (ctx, p, pop) returns a
pointer of type
PGAIndividual to the individual (the string and associated fields)
specified by (p, pop). PGAIndividual is a structure, one of the
fields of which is chrom, a void pointer to the string itself.
That pointer, new->chrom, is assigned the address of the memory
allocated by the malloc function. As malloc returns a void
pointer, no cast is necessary.
The value of InitFlag is passed by PGAPack to the user’s string
creation routine. It specifies whether to randomly initialize the string
or set it to zero. By default, PGA_OLDPOP (except for
PGA_TEMP1 and PGA_TEMP1 which are set to zero) is
randomly initialized, and PGA_NEWPOP is set to zero. This
choice may be changed with the PGASetRandomInitFlag() function
discussed in Section Initialization.)
int Mutation (PGAContext *ctx, int p, int pop, double mr) {
ligand *ligand_ptr;
int i, count = 0;
ligand_ptr = (ligand *)PGAGetIndividual (ctx, p, pop)->chrom;
for (i = 0; i < 6; i++)
if (PGARandomFlip (ctx, mr)) {
if (PGARandomFlip (ctx, 0.5))
ligand_ptr->t[i] += 0.1*ligand_ptr->t[i];
else
ligand_ptr->t[i] -= 0.1*ligand_ptr->t[i];
count++;
}
for (i = 0; i < 40; i++)
if (PGARandomFlip (ctx, mr)) {
if (PGARandomFlip (ctx, 0.5))
ligand_ptr->sc[i] += 1;
else
ligand_ptr->sc[i] -= 1;
count++;
}
return (count);
}
Figure Mutation for Structure Data Type
contains the mutation function Mutation for the ligand data type.
Each of the 46 genes has a probability of mr of being changed. If a
mutation occurs, Mutation adds or subtracts one tenth to the
existing value of a double, and adds or subtracts one to an int.
void Crossover
(PGAContext *ctx, int p1, int p2, int pop1, int t1, int t2, int pop2)
{
int i;
ligand *parent1, *parent2, *child1, *child2;
double pu;
parent1 = (ligand *)PGAGetIndividual (ctx, p1, pop1)->chrom;
parent2 = (ligand *)PGAGetIndividual (ctx, p2, pop1)->chrom;
child1 = (ligand *)PGAGetIndividual (ctx, t1, pop2)->chrom;
child2 = (ligand *)PGAGetIndividual (ctx, t2, pop2)->chrom;
pu = PGAGetUniformCrossoverProb (ctx);
for (i = 0; i < 6; i++)
if (PGARandomFlip (ctx, pu)) {
child1->t[i] = parent1->t[i];
child2->t[i] = parent2->t[i];
} else {
child1->t[i] = parent2->t[i];
child2->t[i] = parent1->t[i];
}
for (i = 0; i < 40; i++)
if (PGARandomFlip (ctx, pu)) {
child1->sc[i] = parent1->sc[i];
child2->sc[i] = parent2->sc[i];
} else {
child1->sc[i] = parent2->sc[i];
child2->sc[i] = parent1->sc[i];
}
}
Figure Crossover for Structure Data Type
contains the crossover function Crossover, which implements uniform
crossover for the ligand data type. The lines
parent1 = (ligand *)PGAGetIndividual (ctx, p1, pop1)->chrom;
parent2 = (ligand *)PGAGetIndividual (ctx, p2, pop1)->chrom;
child1 = (ligand *)PGAGetIndividual (ctx, t1, pop2)->chrom;
child2 = (ligand *)PGAGetIndividual (ctx, t2, pop2)->chrom;
are worthy of mention. Each implements in one line what the two lines
new = PGAGetIndividual (ctx, p, pop);
string = (ligand *)new->chrom;
in Mutation for Structure Data Type did. Either style is
acceptable. PGAGetIndividual() returns a pointer whose chrom
field (a void pointer) is cast to the ligand data type.
int DuplicateString (PGAContext *ctx, int p1, int pop1, int p2, int pop2)
{
void *a, *b;
a = PGAGetIndividual (ctx, p1, pop1)->chrom;
b = PGAGetIndividual (ctx, p2, pop2)->chrom;
return (!memcmp (a, b, sizeof (ligand)));
}
PGAHash HashString (PGAContext *ctx, int p, int pop)
{
void *lig = PGAGetIndividual (ctx, p, pop)->chrom;
return PGAUtilHash (lig, sizeof (ligand), PGA_INITIAL_HASH);
}
Figure Duplicate Testing for Structure Data Type
contains the code for DuplicateString, which checks for duplicate
ligand structures. It uses the ANSI C memcmp function for this
purpose. In figure Hashing for Structure Data Type
the code for the hashing function is shown. It uses the utility function
PGAUtilHash() for computing the hash over the user-defined data
structure.
double Evaluate (PGAContext *ctx, int p, int pop, double *aux)
{
int i, j;
double x[6];
int sc[40];
PGAIndividual *ind;
ligand *lig;
lig = (ligand *)PGAGetIndividual (ctx, p, pop)->chrom;
for (i = 0; i < 6; i++)
x[i] = lig->t[i];
for (i = 0; i < 40; i++)
sc[i] = lig->sc[i];
return energy (x, sc);
}
Figure Evaluation Function for Structure Data Type contains the evaluation
function for this example. It again uses PGAGetIndividual() to map
(p, pop) into a pointer to the string of interest. For user data
types, PGAPack does not provide a PGAGetUserAllele function, so
access to the allele values is made directly through the pointer.
MPI_Datatype BuildDT (PGAContext *ctx, int p, int pop)
{
int idx = 0;
int counts [PGA_MPI_HEADER_ELEMENTS + 2];
MPI_Aint displs [PGA_MPI_HEADER_ELEMENTS + 2];
MPI_Datatype types [PGA_MPI_HEADER_ELEMENTS + 2];
MPI_Datatype DT_PGAIndividual;
PGAIndividual *P;
ligand *S;
P = PGAGetIndividual (ctx, p, pop);
S = (ligand *)P->chrom;
idx = PGABuildDatatypeHeader (ctx, p, pop, counts, displs, types);
/* Finish the MPI datatype. Every user defined function needs these.
* The stuff internal to PGAPack is already handled by
* PGABuildDatatypeHeader above.
*/
MPI_Get_address (S->t, &displs [idx]);
counts [idx] = 6;
types [idx] = MPI_DOUBLE;
idx++;
MPI_Get_address (S->sc, &displs [idx]);
counts [idx] = 40;
types [idx] = MPI_INT;
idx++;
MPI_Type_struct (idx, counts, displs, types, &DT_PGAIndividual);
MPI_Type_commit (&DT_PGAIndividual);
return DT_PGAIndividual;
}
Figure Message Packing Function for Structure Data Type contains the function
BuildDT that builds an MPI datatype for sending strings to other
processors. Consult an MPI manual for further information.
Hill-Climbing and Hybridization
Hill-climbing heuristics attempt to improve a solution by moving to a better neighbor solution. Whenever the neighboring solution is better than the current solution, it replaces the current solution. Genetic algorithms and hill-climbing heuristics have complementary strong and weak points. GAs are good at finding promising areas of the search space, but not as good at fine-tuning within those areas. Hill-climbing heuristics, on the other hand, are good at fine-tuning, but lack a global perspective. Practice has shown that a hybrid algorithm that combines GAs with hill-climbing heuristics often results in an algorithm that can outperform either one individually.
There are two general schemes for creating hybrid algorithms. The simplest is to run the genetic algorithm until it terminates and then apply a hill-climbing heuristic to each (or just the best) string. The second approach is to integrate a hill-climbing heuristic with the genetic algorithm. Choices to be made in the second case include how often to apply the hill-climbing heuristic and how many strings in the population to apply it to.
PGAPack supports hybrid schemes in the following ways:
By passing, the context variable as a parameter to the user’s hill-climbing function, the user has access to solution and parameter values, debug flags, and other information.
The functions
PGAGetBinaryAllele(),PGAGetIntegerAllele(),PGAGetRealAllele(), andPGAGetCharacterAllele()allow the user’s hill-climbing function to read allele values, and the functionsPGASetBinaryAllele(),PGASetIntegerAllele(),PGASetRealAllele(), andPGASetCharacterAllele()allow the user’s hill-climbing function to set allele values explicitly.The functions
PGAGetRealFromBinary(),PGAGetRealFromGrayCode(),PGAGetIntegerFromBinary(), andPGAGetIntegerFromGrayCode()allow the user’s hill-climbing function to read integer or real numbers encoded as binary or Gray code strings.The functions
PGAEncodeRealAsBinary(),PGAEncodeRealAsGrayCode(),PGAEncodeIntegerAsBinary(), andPGAEncodeIntegerAsGrayCode()allow the user’s hill-climbing function to encode integer or real numbers as binary or Gray code strings.The functions
_PGAGetEvaluation()and_PGASetEvaluation()allow the user’s hill-climbing function to get and set evaluation function values, andPGASetEvaluationUpToDateFlag()andPGAGetEvaluationUpToDateFlag()to get and set the flag that indicates whether an evaluation function value is up to date. These functions have an optional fifth argumentaux, that allows to get or set the auxiliary evaluations, see section String Evaluation and Fitness.
One way to run a hybrid GA and use PGARun() is to use the
PGASetUserFunction() discussed in Chapter Custom Usage: Native Data Types to
specify a user function to be called at the end of each GA iteration. A
more flexible approach would be for the user to call the high-level
PGAPack functions, and their hillclimber to explicitly specify the steps
of the hybrid GA.
Figure Hill-Climbing Heuristic for Maxbit Example is a version of the Maxbit
problem given in Section Maxbit Problem in C. It uses the
hill-climbing function hillclimb, which is called after the
recombination step. It randomly selects a gene to set to one. Note the
PGASetEvaluationUpToDateFlag() call. It sets the flag that indicates
the evaluation function is not current with the string (since the string
was changed). It is critical that this flag be set when the user
changes a string, since the value of this flag determines whether
PGAEvaluate() will invoke the user’s function evaluation routine.
#include "pgapack.h"
double evaluate (PGAContext *, int, int, double *aux);
void hillclimb (PGAContext *, int);
int main (int argc, char **argv)
{
PGAContext *ctx;
ctx = PGACreate (&argc, argv, PGA_DATATYPE_BINARY, 100, PGA_MAXIMIZE);
PGASetUp (ctx);
PGAEvaluate (ctx, PGA_OLDPOP, evaluate, NULL);
PGAFitness (ctx, PGA_OLDPOP);
while (!PGADone (ctx, NULL)) {
PGASelect (ctx, PGA_OLDPOP);
PGARunMutationAndCrossover (ctx, PGA_OLDPOP, PGA_NEWPOP);
hillclimb (ctx, PGA_NEWPOP);
PGAEvaluate (ctx, PGA_NEWPOP, evaluate, NULL);
PGAFitness (ctx, PGA_NEWPOP);
PGAUpdateGeneration (ctx, NULL);
PGAPrintReport (ctx, stdout, PGA_OLDPOP);
}
PGADestroy (ctx);
return 0;
}
void hillclimb (PGAContext *ctx, int pop)
{
int i, p, popsize, stringlen;
popsize = PGAGetPopSize (ctx);
stringlen = PGAGetStringLength (ctx);
for (p=0; p<popsize; p++) {
i = PGARandomInterval (ctx, 0, stringlen-1);
PGASetBinaryAllele (ctx, p, pop, i, 1);
PGASetEvaluationUpToDateFlag (ctx, p, pop, PGA_FALSE);
}
}
Parallel Aspects
This chapter assumes familiarity with the background material in Appendix Parallelism Background. It also assumes that a parallel version of PGAPack was built and that programs are linked with an MPI library.
PGAPack supports parallel and sequential implementations of the single population global model (GM). The parallel implementation uses a controller/responder algorithm in which one process, the controller, executes all steps of the genetic algorithm except the function evaluations. The function evaluations are executed by the responder processes 4.
Basic Usage
Both sequential and parallel versions of PGAPack may be run by using
PGARun(). The choice of sequential or parallel execution depends on
the number of processes specified when the program is started. If one
process is specified, the sequential implementation of the GM is used
(even in a parallel version of PGAPack). If two or more processes are
specified, the parallel implementation of the GM is used. The examples
in Chapter Examples can all be run in parallel by
specifying more than one process at startup.
The specification of the number of processors is done at run time. The
actual format of the specification depends on the MPI implementation and
computer used (see Appendix Parallelism Background for some
examples). PGARun() uses the default MPI communicator,
MPI_COMM_WORLD. This specifies that all processes specified at
startup participate in the computation: one as the controller process, the
others as responder processes. A different communicator may be specified
with PGASetCommunicator() with parameters (ctx, comm), where
comm is an MPI communicator.
PGARun() is really a “wrapper” function that calls PGARunGM()
with the MPI_COMM_WORLD communicator. The user may call PGARunGM()
directly, that is,
PGARunGM (ctx, evaluate, MPI_COMM_WORLD)
where evaluate is the name of the user’s evaluation function and the
third argument is an MPI communicator. Note that the communicator
specified by PGASetCommunicator() does not affect
PGARunGM() since the communicator is specified as function argument.
Explicit Use
In general, explicit use of the parallel features is more complicated
than in the case of sequential functions. This is because the user’s
program must coordinate the execution threads of multiple processes.
PGARunGM() encapsulates all that is necessary into one routine, and
parts of its source code may serve as a useful starting point if one
wishes to develop an explicitly parallel program. The parallel functions
in PGAPack may be viewed as a hierarchy with PGARun() and
PGARunGM() at the top of the hierarchy, PGAEvaluate() next,
PGASendIndividual(), PGAReceiveIndividual(), and
PGASendReceiveIndividual() next, and PGABuildDatatype() at the
bottom of the hierarchy.
PGAGetRank() with parameters (ctx, comm) returns the rank of
the process in communicator comm. If comm is NULL it returns 0.
PGAGetNumProcs() with parameters (ctx, comm) returns the
number of processes in communicator comm. If comm is NULL it
returns 1.
The type of algorithm used to execute PGAEvaluate()
will depend on the number of processes in the communicator comm. If
it is NULL or contains one process, a sequential implementation will
be used. If more than one process is specified it will execute a
controller/responder evaluation of the strings in population pop that
require evaluation by applying, f, the user’s evaluation function.
PGAEvaluate should be called by all processes in communicator
comm.
PGASendIndividual() with parameters (ctx, p, pop, dest, tag, comm)
will send string p in population pop to process dest. The
tag is used to identify the message, and comm is an MPI
communicator. This function calls MPI_Send() to perform the
actual message passing. In addition to string p itself, the
evaluation function value, fitness function value, and evaluation status
flag are also sent.
PGAReceiveIndividual() is the complementary function to
PGASendIndividual(). For example, PGAReceiveIndividual()
with parameters (ctx, p, pop, source, tag, comm, status) will store
in location p in population pop the string and fields of the
individual sent from process source with the MPI tag tag and MPI
communicator comm. status is an MPI status vector.
PGASendReceiveIndividual() combines the functionality of
PGASendIndividual() and PGAReceiveIndividual(). This may
be useful in avoiding potential deadlock on some systems. For example
PGASendReceiveIndividual
(ctx, sp, spop, dest, stag, rp, rpop, source, rtag, comm, status);
Here, sp is the index of the string in population spop to send to
process dest with tag stag. The string received from process
source with tag rtag is stored in location rp in population
rpop. comm and status are the same as defined earlier.
PGABuildDatatype() with parameters (ctx, p, pop) packs
together the string and fields that PGASendIndividual(),
PGAReceiveIndividual(), and PGASendReceiveIndividual()
send and receive. The result is of type MPI_Datatype.
Example
Figure Simple Parallel Example of Explicit Usage is a parallel
version of the example in Figure Simple Example of Explicit Usage.
Since we now have multiple processes executing the program at the same
time, we must coordinate each ones execution. In the example, the controller
process (the one with rank 0 as determined by PGAGetRank()) executes
all functions, and the responder processes execute only those functions that
take a communicator as an argument. Note that this example will execute
correctly even if only one process is in the communicator.
#include "pgapack.h"
double evaluate (PGAContext *ctx, int p, int pop, double *aux);
int main (int argc, char **argv)
{
PGAContext *ctx;
int rank;
ctx = PGACreate (&argc, argv, PGA_DATATYPE_BINARY, 100, PGA_MAXIMIZE);
PGASetUp (ctx);
rank = PGAGetRank (ctx, MPI_COMM_WORLD);
PGAEvaluate (ctx, PGA_OLDPOP, evaluate, MPI_COMM_WORLD);
if (rank == 0)
PGAFitness (ctx, PGA_OLDPOP);
while (!PGADone (ctx, MPI_COMM_WORLD)) {
if ( rank == 0 ) {
PGASelect (ctx, PGA_OLDPOP);
PGARunMutationAndCrossover (ctx, PGA_OLDPOP, PGA_NEWPOP);
}
PGAEvaluate (ctx, PGA_OLDPOP, evaluate, MPI_COMM_WORLD);
if ( rank == 0 )
PGAFitness (ctx, PGA_NEWPOP);
PGAUpdateGeneration (ctx, MPI_COMM_WORLD);
if ( rank == 0 )
PGAPrintReport (ctx, stdout, PGA_OLDPOP);
}
PGADestroy (ctx);
return 0;
}
Performance
The parallel implementation of the GM will produce the same result as
the sequential implementation, usually faster, except if the random
number generator is used inside function evaluations (like in examples
examples/c/dejong and examples/fortran/dejong in function
dejong4 which adds random gaussian noise). However, the parallel
implementation varies with the number of processes. If two processes are
used, both the controller process and the responder process will compute the
function evaluations. If more than two processes are used, the controller is
responsible for bookkeeping only, and the responders for executing the
function evaluations. In general, the speedup obtained will vary with
the amount of computation associated with a function evaluation and the
computational overhead of distributing and collecting information to and
from the responder processes.
The speedup that can be achieved with the controller/responder model is limited by the number of function evaluations that can be executed in parallel. This number depends on the population size and the number of new strings created each generation. For example, if the population size is 100 and 100 new strings are created each GA generation, then up to 100 processors can be put to effective use to run the responder processes. However, with the default rule of replacing only 10% of the population each GA generation, only 10 processors can be used effectively.
Fortran Interface
PGAPack is written entirely in ANSI C. A set of interface functions, also written in C, is designed to be called by Fortran programs and then call the “real” C routine. This mechanism provides most of PGAPack’s functionality to Fortran programs. The following list contains most major differences between C and Fortran. Additional, machine-specific idiosyncrasies are noted in Appendix Machine Idiosyncrasies.
The
Makefiles for the Fortran examples (in./examples/fortranand./examples/mgh) may need to be changed if your Fortran compiler does not support the-Imechanism for specifying the include file search path. You will need to copy or set up a symbolic link to./include/pgapackf.hfrom the directory you are compiling a Fortran program in if this is the case.Since C pointers are stored in Fortran integers, we must make sure the integers are large enough to hold a C pointer. In all examples we currently declare the context variable as
integer,parameter :: k18 = selected_int_kind(18) integer(kind=k18) ctx
This requests an integer that can hold values from \(-10^{18}\) to \(10^{18}\). Since \(2^{63}\approx 9*10^{18}\) this should select a 64-bit integer which is guaranteed to be large enough for a 64-bit pointer. On unusual architectures this may not be enough to make sure that the integer can hold the context pointer. The same is true for requesting an MPI communicator with
PGAGetCommunicator()and passing the result, e.g., toPGAGetRank(). This also needs a variable large enough to hold the communicator on some MPI implementations. Note that previous implementations usedinteger*8which according to a stackoverflow article [STO10] is a common extension but is not and was never Fortran syntax. You may run into problems if your Fortran compiler does not support this construct (e.g. a compiler only supporting Fortran-77) in which case the non-standardinteger*8may help.PGACreatetakes only three arguments in Fortran (notargcorargvas in C).The Fortran include file is
pgapackf.hand should be included in any Fortran subroutine or function that calls a PGAPack function, to ensure correct typing and definition of functions and symbolic constants.If a C function returns one of
int,double, or pointer, the corresponding Fortran function returns aninteger,double precision, orinteger, respectively. If the C function isvoidit is implemented as a Fortran subroutine.When supplying function arguments, a C
intcorresponds to a Fortraninteger, and a Cdoublecorresponds to a Fortrandouble precision. For example, to set the crossover probability to 0.6, usecall PGASetCrossoverProb (ctx, 0.6d0)
or
double precision pc pc = 0.6 call PGASetCrossoverProb (ctx, pc)
Gene indices are \([0,L-1]\) in C, and \([1,L]\) in Fortran, where \(L\) is the string length.
Population member indices are \([0,N-1]\) in C, and \([1,N]\) in Fortran, where \(N\) is the population size.
Fortran does not support command line arguments (Section Command-Line Arguments).
Fortran allows custom usage with native data types (Chapter Custom Usage: Native Data Types), but not with new data types (Chapter Custom Usage: New Data Types).
In the
MPICHimplementation of MPI, the Fortran and C versions ofMPI_Initare different. If the main program is in C, then the C version ofMPI_Initmust be called. If the main program is in Fortran, the Fortran version ofMPI_Initmust be called. Therefore, Fortran users of PGAPack withMPICHmust callMPI_Initthemselves sincePGACreate(), which callsMPI_Initif users haven’t called it themselves, is written in C. It is unclear if this is still the case today.
Debugging Tools
0 |
Trace all debug prints |
11 |
Trace high-level functions |
12 |
Trace all function entries |
13 |
Trace all function exits |
20 |
Trace high-level parallel functions |
21 |
Trace all parallel functions |
22 |
Trace all send calls |
23 |
Trace all receive calls |
30 |
Trace Binary functions |
32 |
Trace Integer functions |
34 |
Trace Real functions |
36 |
Trace Character functions |
40 |
Trace population creation functions |
42 |
Trace select functions |
44 |
Trace mutation functions |
46 |
Trace crossover functions |
48 |
Trace function evaluation functions |
50 |
Trace fitness calculation functions |
52 |
Trace duplicate checking functions |
54 |
Trace restart functions |
56 |
Trace reporting functions |
58 |
Trace stopping functions |
60 |
Trace sorting functions |
62 |
Trace random number functions |
64 |
Trace system routines |
66 |
Trace utility functions |
80 |
Trace memory allocations |
82 |
Trace variable print statements |
PGAPack has a sophisticated built-in trace facility that is useful for
debugging. When the facility is invoked, print statements to stdout
allow the programmer to trace the sequence of functions
PGAPack executes. Due to the negative impact on performance this
facility is not available by default. Instead, you must explicitly
enable tracing when configuring PGAPack with the -debug flag.
The trace facility uses the concept of a debug level. For example,
executing the Maxbit example
(Figure PGAPack C Program for the Maxbit Example) with a debug
level of 12, maxbit -pgadbg 12, will print the output shown in
Figure PGAPack Partial Trace Output for Maxbit Example. The “0:” is the process rank.
This is followed by the name of a PGAPack function and the “action” that
caused the print statement to execute. In this case, the action is
entering the function. Note that the rank printed for a process is
always its rank in the MPI_COMM_WORLD communicator, even if
another communicator was set.
0: PGACreate : Entered
0: PGASetRandomSeed : Entered
0: PGASetMaxGAIterValue : Entered
0: PGASetUp : Entered
:
0: PGARun : Entered
0: PGARunSeq : Entered
0: PGAEvaluate : Entered
0: PGAFitness : Entered
0: PGAGetStringLength : Entered
:
Tracing is enabled by specifying one or more debug levels to trace. A list of debug levels is given in Table Debug Levels in PGAPack. Not all debug level values are currently used. The values 1–10 are reserved for users as described below.
C programmers may set the debug level from the command line using either
-pgadbg <debug_level> or -pgadebug <debug_level>. Several forms
of the <debug_level> argument are allowed. -pgadbg 12 will trace
entering all high-level functions as shown in
Figure PGAPack Partial Trace Output for Maxbit Example. -pgadbg 12,13 or
-pgadbg 12-13 will trace entering and exiting of all high-level
functions. The command line option -pgahelp debug will list the
debug level options and then exit.
Fortran (and C) programmers may access the trace facility via function
calls. The function PGASetDebugLevel() may be called to set a debug
level. For example,
call PGASetDebugLevel(ctx, 12)
would produce the same output shown in Figure PGAPack Partial Trace Output for Maxbit Example.
PGAClearDebugLevel() with parameter 12 will clear prints
associated with debug level 12. PGAPrintDebugOptions() will print
the list of available debug options.
The function PGASetDebugLevelByName() will turn on debugging of the
named function. For example, PGASetDebugLevelByName(ctx, "PGACrossover")
will enable all the trace prints of PGACrossover().
PGAClearDebugLevelByName() will disable the tracing of the
specified function.
Users can use the trace facility in their own functions (e.g., their
evaluation function) in two ways. First, they can insert
PGADebugPrint() function calls in their functions using one of the
symbolic constants defined in the header file pgapack.h. These
are documented in group Debugging Constants. Events for which
debug output can be printed include
entering a function, exiting a function, allocating memory, print a
variable’s value, and sending or receiving a string, respectively.
For example,
PGADebugPrint (ctx, PGA_DEBUG_ENTERED, "MyFunc", "Entered", PGA_VOID, NULL)
will print the line:
0: MyFunc : Entered
when the debug level of 12 is specified.
PGADebugPrint (ctx, PGA_DEBUG_PRINTVAR, "MyFunc", "i = ", PGA_INT, (void *)&i)
will print the line:
0: MyFunc : i = 1
when the debug level of 82 is specified. Users can also use the reserved debug levels of 1–10 to customize the trace facilities for use in their own functions. For example
PGADebugPrint (ctx, 5, "MyFunc", "After call to MyCleanUp", PGA_VOID, NULL);
will print the line:
0: MyFunc : After call to MyCleanUp
when the debug level of five is specified.
Note that we use MPI_COMM_WORLD (1) for the random number seed and
(2) for PGADebugPrint() calls.
- 1
PGADestroy()will also callMPI_finalize, if MPI was started byPGACreate().- 2
Even though only ten bits are necessary to encode 564, the user may want to allow the GA any value between \([0,4095]\), hence the twelve bits.
- 3
Technically, this is known as a Hamming cliff.
- 4
In the special case of exactly two processes, the controller executes function evaluations as well.
- 5
More generally, these issues arise whenever the size of a Fortran integer is less than the size of a pointer.